区间
区间:所有在两个已知数之间的数。
例子:所有在 1 和 6 之间的数是个区间
所有的数?
对。所有在两个数值之间的实数。
例子:2 到 4 的区间包括这些数:
| 2.1 | 2.1111 | 2.5 | 2.75 | 2.80001 |
π
|
7/2 | 3.7937 |
还有很多!
包括两端的数吗?
…… 可以包括 …… 也可以不包括 …… 需要说明!
例子:"大至 20千克的箱子是允许的"
如果你的箱子是刚好 20千克 …… 允许吗?
不清楚。
有三个方法来清楚说明:
- 不等式
- 实数直线
- 区间符号
不等式
以不等式表达:
- > 大于
- ≥ 大于或等于
- < 小于
- ≤ 小于或等于
像这样:
例子:x ≤ 20
这样说:"x 小于或等于 20"
意思是:大至并包括 20
区间符号
以 "区间符号" 表达就是写出区间两端的数值,再用:
- [ ] 方括号来代表包括端值,或
- ( )圆括号来代表不包括
像这样:
例子:(5, 12]
意思是从 5 到 12,不包括 5,但包括 12
实数直线
以实数直线表达,用粗线来代表包括的数值,并且:
- 用实心圆点来代表包括端值,或
- 空心圆点来代表不包括端值
像这样:
例子:

意思是所有在 0 和 20 之间的数,不包括 0,但包括 20
三个方法在一起
这是三个方法放在一起的列表(区间是 1 到 2):
| 从 1 | 到 2 | ||||
| 包括 1 | 不包括 1 | 不包括 2 | 包括 2 | ||
| 不等式: | x ≥ 1
"大于 或等于" |
x > 1
"大于" |
x < 2
"小于" |
x ≤ 2
"小于 或等于" |
|
| 实数直线: | 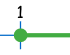 |
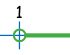 |
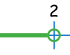 |
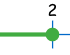 |
|
| 区间符号: | [1 | (1 | 2) | 2] | |
例子:要包括 1 及 不包括 2:
| 不等式: |
x ≥ 1 并且 x < 2 一起:1 ≤ x < 2
|
| 实数直线: |   |
| 区间符号: | [1, 2) |
更多例子
例一、"没有比 ¥10贵的优惠活动"
意思是大至并包括 ¥10。
价钱应该大于 ¥0.00。
用不等式表示:
价钱 ≤ 10 并且 > 0
一起写:
0 < 价钱 ≤ 10
在实数直线上像这样:
![(0, 10]](images/interval-0-10.gif)
用区间符号就是:
(0, 10]
例二、"参赛者年龄一定要从 14 到 18"岁
所以包括 14岁,并且"年龄是 18"岁就是大至但不包括 19岁。
用不等式就是这样:
14 ≤ 年龄 < 19
在实数直线上是:

用区间符号就是:
[14, 19)
年龄是与别不同的。还没到 19岁生日,我们还是 18岁。虽然在 18½ 年后,最近的年数是 19,我们的年龄还是 18岁。
开与闭
我们有时用"开" 与 "闭" 来显示是否包括端值:
| (a, b) | a < x < b | 开区间 | ||
| [a, b) | a ≤ x < b | 左闭右开区间 | ||
| (a, b] | a < x ≤ b | 左开右闭区间 | ||
| [a, b] | a ≤ x ≤ b | 闭区间 |
这些都是有限区间。也有无限区间。
到(但不超越)无穷大!
我们时常在区间符号中使用无穷大。
无穷大不是个实数,这里它的意思是 "无限延续 ……"
例子:x 大于或等于 3:
[3, +∞)
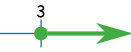
注意我们在无穷大的一端用圆括号,因为我们不能达到无穷大!
有 4个 "单侧无界"区间:
| 区间 | 不等式 | |||
| (a, +∞) | x > a | "大于 a" | ||
| [a, +∞) | x ≥ a | "大于或等于 a" | ||
| (-∞, a) | x < a | "小于 a" | ||
| (-∞, a] | x ≤ a | "小于或等于 a" |
也可以有双侧无界区间:(-∞, +∞)
两个区间
可以有两个(或以上)区间。
|
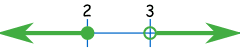
注意:要小心这样的两个区间。 2 ≥ x > 3 这是荒谬的(不能同时小于 2 及大于 3)。 |
并集与交集
上面我们用了 "并集"(符号是 ∪)。
也有 "交集",意思是 "在一个且在另一个"。就是:"两个集的重叠部分"。
交集符号是倒转的英语大写字母 "U":∩
例子:(-∞, 6] ∩ (1, ∞)
第一个区间是 6和以下(包括 6)
第二个区间是 1 以上(但不包括 1).
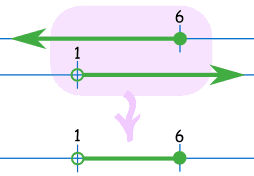
这两个区间的交集(重叠)是从 1 到 6(不包括 1,但包括 6):
(1, 6]
结论
- 区间是所有在两个已知数之间的数。
- 需要显示是否包括头尾两个端值
- 有三个主要方法去显示区间:不等式、实数直线和区间符号。
 错!
错!