虚数
| 虚数的平方是负数。 |
尝试
我们来求一些数的平方,看看能不能得到负数:
不行!永远是正数或零。
我们不能将一个数乘以自己得到负数……
 |
…… 但们可以想象有这样的数(称之为 i): i × i = −1
有什么用?可以用来做什么? |
每边开平方根就得到:
 |
| 意思是 i 是 −1 的平方根。 |
其实这个数很有用,因为 ……
…… 接受 了 i 的存在后,我们可以解答很多
牵涉到负数平方根的问题。
具体地说:
哈!有趣!−9 的平方根是 +9 的平方根乘以 i。
一般来说:
√(−x) = i√x
我们一定要保留 "i",因为
要记得乘以 √−1!
在运算中使用 i,我们就可以得到新的解:
例子:解 x2 = −1
如果只用实数,我们不能解这方程式,但现在用虚数就可以了!
每边开平方根:
答案:x = −i 或 +i
检验:
- (−i)2 = (−i)(−i) = +i2 = −1
- (+i)2 = (+i)(+i) = +i2 = −1

虚数单位
虚数 "单位" (像实数的 1)是 √(−1)(负一的平方根)。
在数学里用 i,在电子学里用 j(因为 "i" 已经用来代表电流,所以就用下一个字母)。
虚数例子
| i | 12.38i | −i | 3i/4 | 0.01i | −i/2 |
虚数不是"虚"无飘渺的
以前虚数曾经被认为是不可能存在的,所以称之为 "虚"数(虚幻的)。
但经过研究后,人们才领悟到虚数其实是很有用并且重要的,因为它填补了数学里的一个缺口……但我们仍然称它为 "虚"数。
这也是 "实数" 这个名称的来源(实不是虚)。
虚数很有用
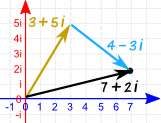
复数
当我们把虚数和实数结合在一起成为复数时,它的用途就更大了。
频谱分析仪
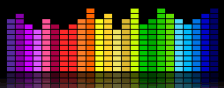
播放音乐时时常会看到的频谱显示就是用复数计算出来的!使用的数学技巧叫 "傅里叶变换"。
我们可以使用复数来对声音做很多有用的运算,例如声音过滤或聆听微弱声音等等。
这个学科叫 "信号处理"。
电学

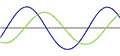
AC(交流电)是随时间按正弦波作周期性变化的电流。
当我们把两个不对称的交流电合并时,计算合并后的电流是非常困难的。
但是,利用复数就可以使得计算简单很多。
虽然结果会含有"虚"电流,但它还是实实在在的电流。

曼德勃罗特集
美丽的曼德勃罗特集(部分如图所示)是基于复数的。
二次方程
![]()
二次方程很有用,
它的解也包含复数
科学,例如量子力学与相对论都使用了复数。
有趣属性
虚数单位 i 有个有趣的属性。它自乘的积在四个答案里"循环重复":
|
所以:
| i = √−1 | i2 = −1 | i3 = −√−1 | i4 = 1 | i5 = √−1 | …… |
例子:i6 是多少?
| i6 | = | i4 × i2 |
| = | 1 × −1 | |
| = | −1 |
这些答案可以在复平面上显示
结论

虚数单位 i 等于负1的平方根
虚数不是"虚"幻的,它实际存在,并且非常有用。