简化平方根
要简化平方根:尽量把平方根符号里面的数变小(但还是个整数):
例子:√8 可以简化为 2√2
你可以用计算器来确定两个数值是相同的!
这是个有用的规则:当 a 和 b 不是负数时:
![]()
应用:
例子(续)
√8 = √(4×2) = √4 × √2 = 2√2
(因为 4 的平方根是 2)
再来一个例子:
例子:简化 √12
12 是 4 乘 3:
√12 = √(4 × 3)
使用规则:
√(4 × 3) = √4 × √3
4 的平方根是 2:
√4 × √3 = 2√3
所以 √12 可以简化为 2√3
一行做好:
例子:简化 √18
√18 = √(9 × 2) = √9 × √2 = 3√2
把数字分解为因数(最好是质因数)会很有帮助:
例子:简化 √6 × √15
首先,把数字合并成一项:
√6 × √15 = √(6 × 15)
分解因数:
√(6 × 15) = √(2 × 3 × 3 × 5)
有两个 3,所以可以"移到平方根外面":
√(2 × 3 × 3 × 5) = √(3 × 3) × √(2 × 5) = 3√10
分数
分数的规则也差不多:
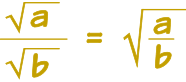
例子:简化 √30 / √10
把数合并:
√30 / √10 = √(30 / 10)
然后简化:
√(30 / 10) = √3
比较复杂的例子
例子:简化 (√20 × √5) / √2
慢慢地逐步看:
(√20 × √5)/√2
(√(2 × 2 × 5) × √5)/√2
(√2 × √2 × √5 × √5)/√2
√2 × √5 × √5
√2 × 5
5√2
例子:简化 2√12 + 9√3
先简化 2√12:
2√12 = 2 × 2√3 = 4√3
每项都有 √3,可以加起来:
4√3 + 9√3 = (4+9)√3 = 13√3
不尽根数
注意:不能再简化的方根叫不尽根数。所以 √3 是个不尽根数。但 √4 = 2 不是不尽根数。