二次方程
二次方程例子：
二次方程的图很漂亮，像这样：
一般形式
二次方程式的一般形式是这样的：
|
更多例子：
| 2x2 + 5x + 3 = 0 | 在这例子， a=2、b=5 和 c=3 | |
| x2 − 3x = 0 |
这个有点巧妙：
|
|
| 5x − 3 = 0 | 哎呀！ 这个 不是 二次方程：没有 x2 换句话说，a=0，就不是二次式） |
隐藏的二次方程！
二次方程的 "一般形式" 是
ax2 + bx + c = 0
但二次方程有时看上去不是这样的！例如：
| 乔装 | → | 一般形式 | a、b 和 c |
|---|---|---|---|
| x2 = 3x − 1 | 把所有的项移到左边 | x2 − 3x + 1 = 0 | a=1、b=−3、c=1 |
| 2(w2 − 2w) = 5 | 展开（拆开 括号）， 把5移到左边 |
2w2 − 4w − 5 = 0 | a=2, b=−4, c=−5 |
| z(z−1) = 3 | 展开，把3移到左边 | z2 − z − 3 = 0 | a=1, b=−1, c=−3 |
 |
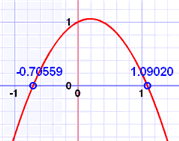来玩玩来玩玩"二次方程探测器"。你可以看到：
|
怎样解方程？
二次方程的 "解" 是方程等于零的地方。
二次方程通常有两个解（"零点"），（如上图）
有三个解二次方程的方法：
一、我们可以 因式分解二次式 （找什么相乘可以得到这二次方程）
二、我们可以 配方，或
三、我们可以用这专用的 二次公式:
![二次公式：x = [ -b (+-) sqrt(b^2 - 4ac) ] / 2a](images/quadratic-formula.svg)
你只需代入 a、b 和 c 的值，然后算根的值。
我们现在来具体看看这个方法。
关于二次公式
正/负
先看看这个 正/负 号：±。
|
± 的意思是有两个答案：
这是为什么有两个答案。 |
|
![二次公式：x = [ -b + sqrt(b^2 - 4ac) ] / 2a 和 x = [ -b - sqrt(b^2 - 4ac) ] / 2a](images/quadratic-formula-two.gif)
可是，有时候没有两个实数答案，我们看看 "判别式" 便知道：
判别式
看到上面公式里的 b2 − 4ac 吗？这便是 判别式，因为它可以 "判别" 不同种类的可能答案：
复解？这个后边再谈。我们先看看怎样去用这个公式。
二次公式应用
把 a、b 和 c 的值代入二次公式，然后计算答案。
例子：解 5x² + 6x + 1 = 0
| 系数是： | a = 5、b = 6、c = 1 | |
| 二次公式： | x = −b ± √(b2 − 4ac) 2a | |
| 代入 a、b 和 c： | x = −6 ± √(62 − 4×5×1) 2×5 | |
| 解： | x = −6 ± √(36 − 20) 10 | |
| x = −6 ± √(16) 10 | ||
| x = −6 ± 4 10 | ||
| x = −0.2 或 −1 |
 |
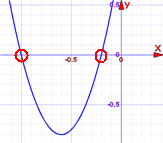答案： x = −0.2 或 x = −1
如图。 |
| 检验 -0.2: | 5×(−0.2)² + 6×(−0.2) + 1 = 5×(0.04) + 6×(−0.2) + 1 = 0.2 − 1.2 + 1 = 0 |
| 检验 -1: | 5×(−1)² + 6×(−1) + 1 = 5×(1) + 6×(−1) + 1 = 5 − 6 + 1 = 0 |
复解？
当判别式（b2 − 4ac 的值）是负数时，方程的解便是 复解……这又是什么意思呢？
意思是答案会含有 虚数。（一头雾水！）
例子：解 5x² + 2x + 1 = 0
| 系数是： | a = 5, b = 2, c = 1 | |
| 注意： 判别式 是负数： | b2 − 4ac = 22 − 4×5×1 = -16 | |
| 用二次公式： | x = −2 ± √(−16) 10 | |
| -16 的平方根是 4i (i 是 √-1，去 虚数 来了解更多） |
||
| 结果： | x = −2 ± 4i 10 | |
 |
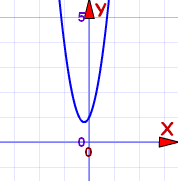答案： x = −0.2 ± 0.4i
图不经过 x轴。这就是为什么解是复数。 |
这其实更为简单：我们不需要做计算，只要写下 −0.2 ± 0.4i 就行了。
总结
- 二次方程的一般形式：ax2 + bx + c = 0
- 二次方程可以被 因式分解
- 二次公式：x = −b ± √(b2 − 4ac) 2a
- 当判别式(b2−4ac)为：
- 正数时，方程有 2 个实解
- 零时，方程有一个实解
- 负数时，方程有 2 个复解