配方法
"配方"是……
| ……拿一个像这样的二次方程: | 把它转化为: | |
ax2 + bx + c = 0 |
a(x+d)2 + e = 0 |
| 如果你没有时间看下去,我可以告诉你: | d = b2a | |
| 并且: | e = c − b24a |
但若你有时间,让我教你怎样自己"配方"。
配方法
假设我们有一个简单的式子,像x2 + bx。x在式子里出现两次,这相当复杂。怎办?
借用几何的理念,我们可以改变它,像这样:
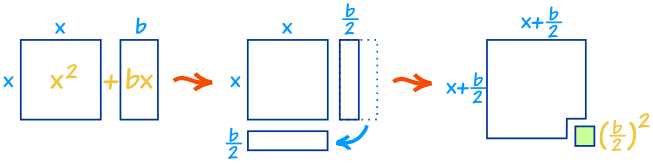
x2 + bx可以几乎重排成一个正方形……
……我们可以搭配上(b/2)2来完成这个正方形
在代数这是:
| x2 + bx | + (b/2)2 | = | (x+b/2)2 | |
| "配方" |
只要配上(b/2)2,我们就可以完成正方形。
现在(x+b/2)2里x只出现一次,令处理比较容易。
保持平衡
注意……我们不能只加 (b/2)2,而不把它减去!否则方程便会完全改变。
我们来看看正确做法的例子:
| 开始: | ||
| (在这里"b" 是 6) | ||
配方: |
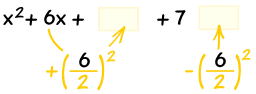
同时,减同一项 |
|
简化,就做好了。 |
||
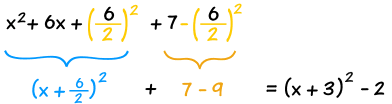 |
||
结果:
x2 + 6x + 7 = (x+3)2 − 2
现在x只出现一次,我们做好了!
捷径
我们来看看我们想要的结果:(x+d)2 + e
展开 (x+d)2 为 x2 + 2dx + d2,所以:
![x^2 + (6x) + [7] 对合 x^2 + (2dx) + [d^2+e]](images/completing-square-expanded.gif)
我们可以"逼"出一个答案出来:
- 我们知道6x会成为2dx,所以d一定是 3
- 我们也知道7会成为 d2 + e = 9 + e,所以e 一定是 −2
得到的结果 (x+3)2 − 2 和上面是一样的!
我们现在来看看一个配方法的应用:解二次方程……
用配方法来解一般二次方程
我们可以用配方法来解一个二次方程(求它何时等于零)。
但一个二次方程可以有系数 a 在x2前面:
ax2 + bx + c = 0
这很容易……先把方程除以 "a",然后继续:
x2 + (b/a)x + c/a = 0
步骤
我们可以用 5 步来解二次方程:
- 一、 把所有项除以 a(x2的系数)。
- 二、 把常数项 (c/a) 移到方程的右边。
- 三、 左边配方,右边也加同项以保持平衡。
现在方程像 (x + p)2 = q,解这个相当容易:
- 四、 取方程两边的平方根。
- 五、 减去左边剩下的数来求x。
例子
以下有两个例子:
例子 1: 解 x2 + 4x + 1 = 0
一、 可以略过因为 x2 的系数是 1
二、 把常数项移到右边:
三、 左边配方,右边也加同项以保持平衡。
(b/2)2 = (4/2)2 = 22 = 4
四、 取方程两边的平方根:
五、 每边减 2:
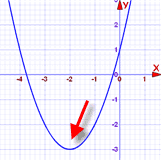
还有一个有趣并且有用的小知识。 做完第三步后,方程是: (x + 2)2 = 3
这方程告诉我们 x2 + 4x + 1 的顶点(转折点)在(-2, -3) |
 |
例子 2:解 5x2 – 4x – 2 = 0
一、 所有项除以 5
二、 把常数项移到右边:
三、 左边配方,右边也加同项以保持平衡:
(b/2)2 = (0.8/2)2 = 0.42 = 0.16
四、 取方程两边的平方根:
五、 每边减 (-0.4) (换句话说,加 0.4):
为什么要"配方"?
为什么要配方?为什么不用二次方程求根公式去解二次方程?
上面讲了一个原因,除了解方程以外,我们还可以知道顶点在哪里。
有时这个方程格式 ax2 + bx + c 可能是一个更大的问题的一部分,把它重排成 a(x+d)2 + e 会让求解更容易,因为 x 只出现一次。
例如, "x" 可能是个函数(像cos(z)),重排后可能可以让我们找到一个更好的解法。
配方也是导出二次方程的求根公式的方法
配方法是你的数学工具箱里的一个工具。
附注: "d"和 "e" 的值
怎样得到在这页面顶部的 d 和 e 的值?
| 开始 | |
| 除以 a | |
| 把 c/a 移到另一边 | |
| 每边加 (b/2a)2 | |
| "配方" | |
| 把所有项移到…… | |
| ……左边 | |
| ……乘以 a,还原 x2的指数 | |
| 我们得到了: | a(x+d)2 + e = 0 |
|
| 其中: | d = b 2a | |
| 并且: | e = c − b2 4a | |
| 和页顶一样! | ||