导出二次公式

二次方程看起来像这样：

二次方程ax^2 + bx + c = 0

我们可以用二次公式来解它：

二次公式：x = [ -b (+-) sqrt(b^2 - 4ac) ] / 2a

公式很神奇，但你其实可以一步一步去了解怎样导出这公式。

一、配方

ax2 + bx + c 有两个 "x" 在里面，这使它比较难解。

但其实有一个方法去把它重排，而使得 "x" 只出现一次。这方法叫 配方法（我建议你先去看看！）。

我们的目标是把二次式变成 x2 + 2dx + d2 的样子，然后我们便可以把它简化成 (x+d)2

好，我们来：

开始 ax^2 + bx + c=0
除以 a x^2 + bx/a + c/a = 0
把 c/a 移到另一边 x^2 + bx/a = -c/a
每边加以 (b/2a)2 x^2 + bx/a + (b/2a)^2 = -c/a + (b/2a)^2

左边 线下是 x2 + 2dx + d2 的格式，"d" 是 "b/2a"
把它重写为：
"配方" (x+b/2a)^2 = -c/a + (b/2a)^2

x 只出现一次了！

二、求解 "x"

我们只需把方程重排为 "x" 单独在左边

开始 (x+b/2a)^2 = -c/a + (b/2a)^2
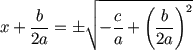取平方根 (x+b/2a) = (+-) sqrt(-c/a+(b/2a)^2)
把 b/2a 移到右边 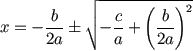x = -b/2a (+-) sqrt(-c/a+(b/2a)^2)

解了！但我们可以再简化：
右边乘以 2a/2a x = [ -b (+-) sqrt(-(2a)^2 c/a + (2a)^2(b/2a)^2) ] / 2a
简化： x = [ -b (+-) sqrt(-4ac + b^2) ] / 2a

哈！这就是二次公式了：
  二次公式：x = [ -b (+-) sqrt(b^2 - 4ac) ] / 2a

 

二次方程 二次式因式分解 配方法 二次方程画图 二次方程实例 二次方程式解算器 代数索引