因式分解二次式
"因式分解" (也叫作"分解因式")一个二次式是去:
找什么式的积等于一个已知的二次式。
叫 "因式分解" 是因为我们去找因式(因式是用来相乘的)
例子
x2 + 3x − 4 的因式是:
(x+4) 和 (x−1)
为什么? 我们把它们相乘来看看:
| (x+4)(x−1) | = x(x−1) + 4(x−1) |
| = x2 − x + 4x − 4 | |
| = x2 + 3x − 4 |
把 (x+4)(x−1) 相乘是叫展开。
实际上,展开和分解是彼此相反的:
展开很容易,但分解有时不简单
 |
这有点像找出什么材料使一个蛋糕好吃。 有时这绝对不明显! |
我们来试试一个我们还不知道因式的例子:
公因式
先看看有没有公因式。
例子:6x2 − 2x = 0 的因式是什么?
2 是 6 和 2 的公因式:
2(3x2 − x) = 0
x 是 x2 和 x 的公因式:
2x(3x − 1) = 0
做好了!因式是 2x 和 3x − 1,
现在我们也可以找二次式等于零的根:
- 当 x = 0 时,2x = 0
- 当 x = 1/3 时,3x − 1 = 0
图如下(留当 x=0 和 x=1/3 时,因式的值是零):
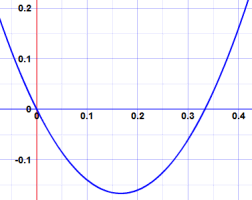
但不是经常都这么容易。。。。。。
猜。。。。。。测
也许我们可以猜一个答案?
例子:2x2 + 7x + 3 的因式是什么?
没有公因式。
我们来猜一个答案,然后测试答案对不对。。。。。。可能我们运气好!
试试 (2x+3)(x+1):
(2x+3)(x+1) = 2x2 + 2x + 3x + 3
= 2x2 + 5x + 3 (错)
再试这个 (2x+7)(x−1):
(2x+7)(x−1) = 2x2 − 2x + 7x − 7
= 2x2 + 5x − 7 (还是不行)
这个呢?(2x+9)(x−1):
(2x+9)(x−1) = 2x2 − 2x + 9x − 9
= 2x2 + 7x − 9 (拿石头砸自己的脚)
糟了!这样要搞多久才能行?
乱打乱撞不是好办法。试试其他的。
简单情况下可用的方法
幸好在简单情况下有一个可用的方法。
当二次方程是这个格式时:
![]()
一、找两个积是等于 give ac 的数(积是 a 乘 c),同时这两个数的和是 b。
例子:2x2 + 7x + 3
ac 是 2×3 = 6,b 是 7
所以我们要找两个数,它们的积是 6,而它们的和是 7
容易!6 和 1 能行 (6×1=6,6+1=7)
可是。。。。。。我们怎样找 6 和 1 出来?
我们可以列出 ac=6 的因数,然后选几对因数加起来试试可不可以得到 b=7.
6 的因数有 1、2、3 和 6。
哈! 1 和 6 的和是 7,并且 6×1=6。
二、以这对因数重写二次式的中间部分:
把 7x 重写为 6x 和 1x:
2x2 + 6x + x + 3
三、把前两项与后两项分开来分解:
前两项 2x2 + 6x 分解为 2x(x+3)
在这例子,后两项 x+3 不能分解
所以:
2x(x+3) + (x+3)
四、若我们没做错,应该有一个很明显的公因式。
在这例子,显而易见,两项都有 (x+3),所以我们可以这样做:
| 开始 | 2x(x+3) + (x+3) | |
| 等于: | 2x(x+3) + 1(x+3) | |
| 故此: | (2x+1)(x+3) |
检测:(2x+1)(x+3) = 2x2 + 6x + x + 3 = 2x2 + 7x + 3 (对了!)
让我们再来很快做第一到第四步,从头到尾,逐步看二次式的变化:
| 2x2 + 7x + 3 |
| 2x2 + 6x + x + 3 |
| 2x(x+3) + (x+3) |
| 2x(x+3) + 1(x+3) |
| (2x+1)(x+3) |
比瞎猜好多了!
再来一个例子:
例子: 6x2 + 5x − 6
一、ac 是 6×(−6) = −36,b 是 5
列出 ac(=36) 的正因数:1、2、3、4、6、9、12、18、36
找两个因数,其中一个要是负数,从而把积成为 −36。试了几个后,我找到 −4 和 9:
−4×9 = −36 和 −4+9 = 5
二、重写 5x,用 −4x 和 9x:
6x2 − 4x + 9x − 6
三、分解头两项和后两项:
2x(3x − 2) + 3(3x − 2)
四、公因式是 (3x − 2)::
(2x+3)(3x − 2)
检测:(2x+3)(3x − 2) = 6x2 − 4x + 9x − 6 = 6x2 + 5x − 6 (对)
找正确的数
最难的一步是找两个因数,要它们的积是 ac,同时它们的和是 b。
这真的是猜测,所以把所有的因数列出来是很重要的。
又一个例子:
例子:ac = −120 和 b = 7
哪两个数的 积是 −120,而 和是 7?
120 的因数是 (正与负):
1、2、3、4、5、6、8、10、12、15、20、24、30、40、60 和 120
找几对因数试试(从中间开始!),看看和是不是 7:
- −10 x 12 = −120,但是 −10+12 = 2 (错)
- −8 x 15 = −120,并且 −8+15 = 7 (行了!)
为什么要分解因式?
因式分解的一个重要用途是用来解二次方程的根(二次式等于零).
分解因式后,我们只需要看两个因式什么时候等于零
例子: 6x2 + 5x − 6 的根(零)是什么?
上面我们已经找到這些因式:
(2x + 3)(3x − 2)
我们可以计算出来,
当 x = −3/2 时,(2x + 3) 亦等于零,
并且
当 x = 2/3 时,(3x − 2) 亦等于零
故此, 6x2 + 5x − 6 的根是:
−3/2 和 2/3
这是 6x2 + 5x − 6 的图,看到它在什么地方等于零吗?
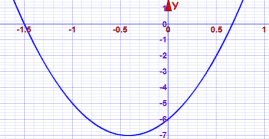
我们可以用算术来检测答案:
当 x = -3/2:6(-3/2)2 + 5(-3/2) - 6 = 6×(9/4) - 15/2 - 6 = 54/4 - 15/2 - 6 = 6-6 = 0
当 x = 2/3:6(2/3)2 + 5(2/3) - 6 = 6×(4/9) + 10/3 - 6 = 24/9 + 10/3 - 6 = 6-6 = 0
画图
我们也可以为二次方程画个图,看看方程在什么地方等于零可以提供一些线索。
例子:(续)
开始:只用 6x2 + 5x − 6 和 这图:

根是大约 x = −1.5 和 x = +0.67,所以我们所以猜方程的根为:
−3/2 和 2/3
由此,我们可以算出因式为 2x + 3 和 3x − 2
不过,一定要检测!0.67 可能不是 2/3!
通用解法
若上面的方法行不通,还有一个通用解法。这解法用二次公式:
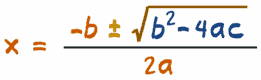
用二次公式来找两个答案 x+ 或 x−(一个是 "±"里的"+"号的答案,另一个是 "−"号的答案),然后把二次式分解为:
a(x − x+)(x − x−)
现在我们用上面的例子来试试:
例子: 6x2 + 5x − 6 的根是什么?
把 a=6, b=5 和 c=−6 代入公式里:
x = (−b ± √[b2 − 4ac]) / 2a
x = (−5 ± √[52 − 4×6×(−6)]) / 2×6
= (−5 ± √[25 + 144]) / 12
= (−5 ± √169) / 12
= (−5 ± 13) / 12
所以两个根是:
x+ = (-5 + 13) / 12 = 8/12 = 2/3,
x− = (-5 − 13) / 12 = −18/12 = −3/2
(和我们上面得到的答案是相同的)
把这些值代入 a(x − x+)(x − x−):
6(x − 2/3)(x + 3/2)
重排来简化:
3(x − 2/3) × 2(x + 3/2) = (3x − 2)(2x + 3)
和上面找到的因式一模一样!
(谢谢 "mathsyperson" 提供部分内容)