代数因式分解
因数
数有因数:
式子(像x2+4x+3)也有因数(叫因式或因子):
因式分解
因式分解(也叫作分解因式)是把式子化为因式:
因式分解:找什么式子的积可以等于一个已知的式子。
就是把一个式子"分拆"为几个式子的积。
例子:分解 2y+6
2 是 2y 和 6 的因式:
- 2y 是 2 × y
- 6 是 2 × 3
所以整个式子可以分解成:
2y+6 = 2(y+3)
2y+6 被 "分解为" 2 和 y+3 两个因式
因式分解也是展开的相反:
公因式
在上面的例子里,2 是 2y 和 6 的公因式
正确的做法是要找到最大公因式,包括变量在内
例子:分解 3y2+12y
首先,3 是 3 和 12 的公因式。
所以可以这样写:
3y2+12y = 3(y2+4y)
但可以做得更好!
3y2 和 12y 也共同的变量 y。
放在一起便是 3y:
- 3y2 是 3y × y
- 12y 是 3y × 4
故此,整个式可以分解为:
3y2+12y = 3y(y+4)
检测: 3y(y+4) = 3y × y + 3y × 4 = 3y2+12y
更复杂的因式分解
因式分解可以很困难!
以上的例子都很简单,但因式分解其实可以很困难。
因为你要猜 什么式子的积 等于已知的一个式子!
 |
这有点像找出什么材料使一个蛋糕好吃。有时这绝对不明显! |
熟能生巧
经验越多就越容易。
例子:分解 4x2 - 9
嗯。。。。。。看不到有什么因式。
可是,若你了解特别二项式乘积,你也许会看到它是 "平方差":
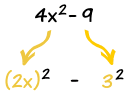
因为 4x2 是 (2x)2,而 9 是 (3)2,
所以:
4x2 - 9 = (2x)2 - (3)2
我们可以用这个平方差公式:
(a+b)(a-b) = a2 - b2
其中 a 是 2x,而 b 是 3。
我们来试试看:
(2x+3)(2x-3) = (2x)2 - (3)2 = 4x2 - 9
行了!
故此,4x2 - 9 的因式是 (2x+3) 和 (2x-3):
答案: 4x2 - 9 = (2x+3)(2x-3)
怎样才可以懂得这样做?做大量练习,并牢记 "恒等式"!
记着这些恒等式
一下是常见的 "恒等式"(包括上面用的 "平方差")。
记着这些会对因式分解很有帮助。
| a2 − b2 | = | (a+b)(a−b) |
| a2 + 2ab + b2 | = | (a+b)(a+b) |
| a2 − 2ab + b2 | = | (a−b)(a−b) |
| a3 + b3 | = | (a+b)(a2−ab+b2) |
| a3 − b3 | = | (a−b)(a2+ab+b2) |
| a3+3a2b+3ab2+b3 | = | (a+b)3 |
| a3−3a2b+3ab2−b3 | = | (a−b)3 |
还有很多,以上只是最常见的。
忠告
分解了的格式通常是最好的格式。
按以下步骤去分解因式:
- "分解出"同类项
- 看看可不可以用以上或其他的恒等式
- 一直做到不能再分解为止
你也可以用电脑!现在有电脑代数系统(叫"CAS"――英语 "Computer Algebra System" 的缩写),例如 Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce等等,它们都可以做因式分解。
更多例子
我说熟能生巧,所以以下有更多的例子给你琢磨:
例子:w4 - 16
4次方? 我们来试试2次方:
w4 - 16 = (w2)2 - 42
对了,这是平方差
w4 - 16 = (w2 + 4)(w2 - 4)
同时,"(w2 - 4)" 也是平方差
w4 - 16 = (w2 + 4)(w + 2)(w - 2)
我不能再分解下去了(除非可以用虚数)。
例子:3u4 - 24uv3
拿走公因数 "3u":
3u4 - 24uv3 = 3u(u3 - 8v3)
然后用立方差:
3u4 - 24uv3 = 3u(u3 - (2v)3)
= 3u(u-2v)(u2+2uv+4v2)
到此为止。
例子:z3 - z2 - 9z + 9
把前两项和后两项分开来做:
z2(z-1) - 9(z-1)
哈!两项都有(z-1),当然要用它:
(z2-9)(z-1)
z2-9 是平方差
(z-3)(z+3)(z-1)
不能继续下去了
