特殊二项式乘积
某些二项式相乘的有趣结果……
二项式
二项式是只有两项的多项式
| 二项式例子 |
乘积
(乘)积 是乘法的结果。
在代数,xy 代表 x 乘以 y
(a+b)(a−b) 的意思是 (a+b) 乘以 (a−b)。我们在这里会时常用这个式子!
特殊二项式乘积
当我们把二项式相乘,结果便是……二项式乘积!
我们会看到三个特殊的二项式相乘的例子……相乘的结果是……特殊二项式乘积。
一、二项式自乘
取二项式的平方(把它与自己相乘)会怎么样?
(a+b)2 = (a+b)(a+b) = ……?
结果:
(a+b)2 = a2 + 2ab + b2
解释如图:
二、减乘以减
计算里面是减号的二项式的平方呢?
(a−b)2 = (a−b)(a−b) = ……?
结果:
(a−b)2 = a2 − 2ab + b2
三、 加乘以减
还有一个特殊情况……这个 (a+b) 乘以 (a−b) 又怎么样?
(a+b)(a−b) = ……?
结果:
(a+b)(a−b) = a2 − b2
这个有趣!结果很简单。
这个公式叫"平方差" (两个平方是 a2 和 b2)。
解释如图:
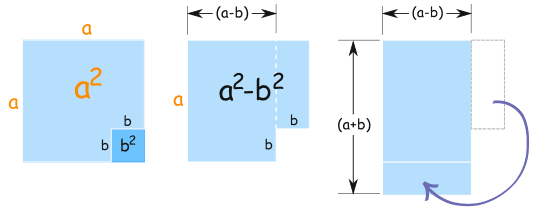 |
a2 − b2 等于 (a+b)(a−b) |
注意:(a−b) 可以是第一项, (a+b) 可以是第二项:
(a−b)(a+b) = a2 − b2
三个情况:
这是上面得到的三个结果:
| (a+b)2 | = a2 + 2ab + b2 | } | "完全平方三项式" |
| (a−b)2 | = a2 − 2ab + b2 | ||
| (a+b)(a−b) | = a2 − b2 | "平方差" |
牢记这些非常有用的公式!
使用
上面我们用 "a" 和 "b",但其实用什么都可以。
例子:(y+1)2
我们用 (a+b)2,以 y 为 "a",1 为 "b":
(y+1)2 = (y)2 + 2(y)(1) + (1)2 = y2 + 2y + 1
例子:(3x−4)2
用 (a-b)2,以 3x 为 "a",4 为 "b":
(3x−4)2 = (3x)2 − 2(3x)(4) + (4)2 = 9x2 − 24x + 16
例子:(4y+2)(4y−2)
我们知道结果是个平方差,因为:
(a+b)(a−b) = a2 − b2
所以:
(4y+2)(4y−2) = (4y)2 − (2)2 = 16y2 − 4
有时候我们可以看到答案:
例子:什么二项式相乘的积是 4x2 − 9?
……看上去像个平方差……对不对?
厉害!
4x2 是 (2x)2, 9 是 (3)2,所以:
4x2 − 9 = (2x)2 − (3)2
用平方差公式:
(a+b)(a−b) = a2 − b2
这样:("a" 是 2x,"b" 是 3):
(2x+3)(2x−3) = (2x)2 v (3)2 = 4x2 − 9
答案是:把 (2x+3) 和 (2x−3) 相乘会得到 4x2 − 9