二次方程
实例

二次方程看起来像这样：

二次方程

在现实世界我们时常可以看到二次方程！

在这里我们会举一些实例，并使用不同的方法去解它们：

每个例子都分成三个阶段：

 

抛球

球、箭、导弹和石头

若你抛一个球（或射箭、发射导弹或抛石头），它飞出去，然后减慢速度，最后越来越快地跌下来……

……二次方程 可以告诉你球在任何时间的位置！

 

例子：抛球

你把球垂直向上抛，球离开你的手时离地3m，速度14 m/s。球在什么时候掉到地上？

不考虑空气阻力，我们可以计算球的位置的高度为以下三项的和：
（注意：t 是时间，以秒为单位）

开始时高度是3m：   3
球以每秒14米（14 m/s）的速度向上飞：   14t
地心引力把球向下拉，把它的高度以 大约 5 米每平方秒 （m/s2） 的率减少：   −5t2
（若你有兴趣：-5t2 是从 -(½)at2，a=9.8 m/s2 简化而来）    

加起来，在时间 t 的速度是：

h = 3 + 14t − 5t2

球掉到地上时高度是零：

3 + 14t − 5t2 = 0

是一个二次方程！写成"一般形式"是这样：

−5t2 + 14t + 3 = 0

我们来解它……

可以用很多方法来解，这里我们用 因式分解的方法：

把所有项乘以 −1 会简单点： 5t2 − 14t − 3 = 0

然后去分解因式。

我们用二次式因式分解的方法："找两个数，要它们的积是 a×c，它们的和是
b"。

a×c = −15，b = −14.

−15 的因数是：−15、−5、−3、−1、1、3、5、15

试试不同的组合，我们找到 −15 和 1：
(−15×1 = −15, −15+1 = −14)
以 −15 和 1 重写中间部分：   5t2 − 15t + t − 3 = 0
因式分解头两项和后两项：   5t(t − 3) + 1(t − 3) = 0
公因式是 (t − 3)：   (5t + 1)(t − 3) = 0
     
两个解是：   5t + 1 = 0 或 t − 3 = 0
    t = −0.2  或  t = 3

"t = −0.2" 是负时间，在这例子里是不可能的。

剩下 "t = 3" 为唯一的答案：

球在离手三秒后掉到地上！

二次图球

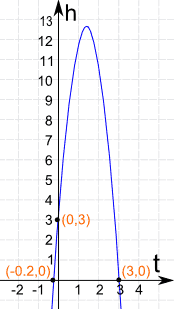
这是 抛物线 h = −5t2 + 14t + 3 的图

它是 球的高度 相对 时间 的图

留意：

(0,3) 当 t=0 （开始）时球在 3m 高

(−0.2,0) 说在球离手前 −0.2秒球是在地上（高度为零）。这是不对的。按常理，我们不管它。

(3,0) 的意思是球离手后 3秒球又在地上了。

还有，球最高抛到差不多 13米。

对这个有兴趣？你可以计算最高点的准确高度！

在二次方程画图有这个方法的详细说明。方法有两步：

用−b/2a求最高点在水平（时间）轴上的值：

然后用这值（1.4）来求高度

  • h = −5t2 + 14t + 3 = −5(1.4)2 + 14 × 1.4 + 3 = 12.8米

    • 离手1.4秒后，球到达12.8米的最高点。

     

    bike  

    例子：新运动自行车

    你设计了一款新运动自行车！

    你打算卖它个上千上万辆来淘你的第一桶金！

    你的成本是：

    （你要卖到国际市场，所以一切用美金来算！）

    自行车需求线图

    你做的市场研究告诉你，售量 会像这个 "需求曲线"：

    其中 "P" 是每辆的价钱

    例如，如果价钱是：

    好了……最好（赚的最多）的价钱是多少？还有，你应该制造多少辆？

    我们来制定一些方程！

    可以卖多少辆要看每辆的价钱，所以我们用价钱 "P" 为变量

    利润 = −200P2 + 92,000P − 8,400,000

    对了，是个二次方程。这次我们用 配方法来解。

    解：−200P2 + 92,000P − 8,400,000 = 0

    一、所有项除以 -200

    P2 – 460P + 42000 = 0

    二、把数字项移到右边：

    P2 – 460P = -42000

    三、左边配方，把等值加到右边以保持平衡：

    (b/2)2 = (−460/2)2 = (−230)2 = 52900

    P2 – 460P + 52900 = −42000 + 52900
    (P – 230)2 = 10900

    四、每边取平方根：

    P – 230 = ±√10900 = ±104 （舍入到最近的整数）
    五、每边减 (-230) （就是每边加 230）：

    P = 230 ± 104 = 126 或 334

    这告诉我们什么？当价钱是 $126 或 $334 时利润是零。

    可是我们想知道的是最大利润……

    刚好在这两个价钱的正中间！$230

    图是这样：

    自行车最大利润图
    利润 = −200P2 + 92,000P − 8,400,000

    最好的价钱是 $230，在这个卖价，情形将会是：

    相当可观！

    例子：小钢框架

    面积=28

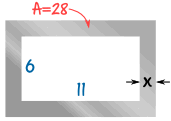
    你的公司将会制造框架作为一个产品的部件。

    我们会从一块矩形的钢片的正中间切出一个矩形的空间，剩下来的便是我们想要的框架。我们需要框架里的钢的面积是 28 cm2

    框架内部的空间的大小是 11 cm × 6 cm

    框架每边的宽度 x 是多少？

    钢片原来（未切前）的面积：

    面积 = (11 + 2x) × (6 + 2x) cm2
    面积 = 66 + 22x + 12x + 4x2
    面积 = 4x2 + 34x + 66

    切出中间（11 × 6 的矩形）之后，剩下来的钢的面积：

    面积 = 4x2 + 34x + 66 − 66
    面积 = 4x2 + 34x

    二次式 4x^2 + 34x

    我们现在用 图 来解这个！

    这是 4x2 + 34x 的图：

    我们用一条水平先来显示想要的面积，28。

    在以下的情况下面积是 28 cm2：

    x 是大约 −9.3 或 0.8

    不可能有负值的宽度（x），所以答案是：

    x = 0.8 cm （大约）

     

    例子：江河畅游

    一个三小时的江河畅游旅程的速度是向上游行驶15km，然后掉头回程。河流的速度是每小时 2 km。邮轮的速度是多少及上游旅程用了多少时间？

    河流草图

    我们要考虑两个速度：邮轮在水里的速度和邮轮相对于陆地的速度：

    因为河流向下游的速度是 2 km/h：

    我们可以把速度转换为时间：

    时间 = 距离 / 速度

    （以 4 km/h 的速度走 8 km 需要 8/4 = 2小时，对不对？）

    旅程总共用了 3 小时：

    总时间 = 向上游时间 + 向下游时间 = 3 小时

    全部集合在一起：

    总时间 = 15/(x−2) + 15/(x+2) = 3 小时

    用代数来解 "x"。

    乘以 (x-2)(x+2) 来移除分数：

    3(x-2)(x+2) = 15(x+2) + 15(x-2)

    展开：

    3(x2−4) = 15x+30 + 15x−30

    移到左边，再简化：

    3x2 − 30x − 12 = 0

    这是个二次方程！这一次我们用 二次公式 来解：

    二次公式

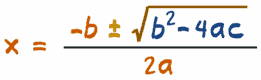
    其中 a、b 和 c 是
    二次方程的 "一般形式" 里的系数：ax2 + bx + c = 0

    解 3x2 - 30x - 12 = 0

    系数是：   a = 3, b = −30 and c = −12
         
    二次公式：   x = [ −b ± √(b2−4ac) ] / 2a
         
    代入 a、b 和 c：   x = [ −(−30) ± √((−30)2−4×3×(−12)) ] / (2×3)
         
    解：   x = [ 30 ± √(900+144) ] / 6
        x = [ 30 ± √(1044) ] / 6
        x = ( 30 ± 32.31 ) / 6
        x = −0.39 或 10.39

     

    答案： x = −0.39 或 10.39 （保留2位小数）

    x =−0.39 不合理，但 b = 10.39 就对了！

    答案：邮轮的速度 = 10.39 km/h （保留2位小数）

    所以向上游的时间 = 15 / (10.39−2) = 1.79 小时 = 1 小时 47分

    向下游的时间 = 15 / (10.39+2) = 1.21 小时 = 1 小时 13分

     

    例子：并联电阻

    两个电阻并联，如图：

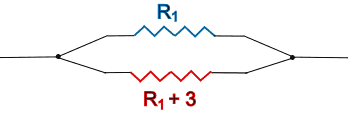
    二次电阻 R1 和 R1+3

    并联后的电阻值为 2欧姆，其中一个电阻的电阻值比另一个大 3欧姆。

    每个电阻的电阻值为多少？

    并联电阻值 "RT" 的公式是：

    1RT   =   1R1 + 1R2

    在这例子里，RT = 2，R2 = R1 + 3

    1 2   =   1 R1 + 1 R1+3

    好，我们来解它：

    把所有项乘以 2R1(R1 + 3)
    来移除分数：    		  

    2R1(R1+3)2 = 2R1(R1+3)R1 + 2R1(R1+3)R1+3
         
    再简化：   R1(R1 + 3) = 2(R1 + 3) + 2R1
         
    展开：   R12 + 3R1 = 2R1 + 6 + 2R1
         
    把项移到左边：   R12 + 3R1 − 2R1 − 6 − 2R1 = 0
         
    简化：   R12 − R1 − 6 = 0

    真巧！（为什么总是这么巧？）又是二次方程！

    不用绞脑汁了，我们用 二次方程解算器 来解。

    R1 不能是负数，所以答案是 R1 = 3欧姆。

    两个电阻的电阻值分别是 3欧姆和 6欧姆。

     

    其他

    二次方程在很多领域都很有用：

    抛物面天线

    抛物面镜面或抛物面天线反射器的形状是以二次方程规定的。

    研究透镜和反射镜时也会用到二次方程。

    很多牵涉到时间、距离和速度的问题都需要用二次方程来解。

     

    二次方程 二次式因式分解 配方法 二次方程画图 二次方程式解算器 代数索引