抛物线

若你踢一个足球（或者射箭、发射导弹或抛石头），它飞出去，然后落下来…… ……沿着抛物线飞行！ （不考虑有空气阻力的影响。）

来试试踢球：

 

定义

抛物线是平面内的曲线，在线上任何一点到：

• 定点（焦点）与
• 定直线（准线）

的距离相等

在纸上画一条直线并在线外画一点作为焦点。

然后用尺来尝试寻找一个到焦点与直线距离相等的点。

画很多这样的点，把他们连起来，就得到一条抛物线了！

 

名称

以下是一些重要的名称：

• 准线 和 焦点（如上）
• 对称轴（穿过焦点，垂直于准线）
• 顶点x （抛物线最弯曲的地方），在焦点与准线的正中间。

 

反射

抛物线有个奇妙的属性：

平行于对称轴的光线经抛物线反射到焦点上。

这就是为什么那点被叫做焦点……

……因为所有的光线都聚焦在那一点上！

抛物线可以应用在：

• 卫星天线、
• 雷达天线、
• 聚焦阳光来加热一点、
• 聚光灯和手电筒的反射镜、
• 等等

 

我们也可以切开一个圆锥来得到抛物线（切面一定要与圆锥的侧面平行）。 所以抛物线是圆锥曲线（圆锥截面）。

方程 把抛物线放在笛卡尔坐标（x-y 图）上： 抛物线的顶点在原点 "O" 上， 对称轴在 x轴上， 抛物线的方程就是： y2 = 4ax

 

不同方向的抛物线的方程是：

y2 = 4ax	y2 = −4ax	x2 = 4ay	x2 = −4ay

抛物面天线的尺寸

如果你要做一个焦点为 200毫米的抛物面天线，天线的尺寸应该是多少？

天线向上比较容易做，所以我们用这个方程：x² = 4ay。

焦点 "a" 是 200，方程就是：

x² = 4ay = 4 × 200 × y = 800y

重排来求高度：

y = x²/800

这是在天线上不同位置的高度：

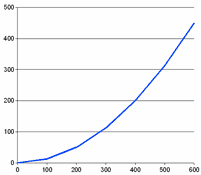	位置（"x"）	高度（"y"）
	0毫米	0.0毫米
	100毫米	12.5毫米
	300毫米	112.5毫米
	400毫米	200.0毫米
	500毫米	312.5毫米
	600毫米	450.0毫米

如果你做了一个，拍个照，告诉我，我会把照片放到网站上！