圆锥曲线

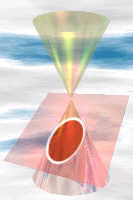
圆锥曲线（也称圆锥截面）：平切圆锥的截面。

 

因此这些曲线都是互相有关联的！

焦点！

这些曲线也可以用一条直线和一点（叫准线 和 焦点）来描述。

如果我们测量以下的距离：

• 从焦点到曲线上任何一点，和
• 从准线垂直到同一点，

这两个距离的比例是不变的。

• 如果是椭圆，比例小于 1
• 如果是抛物线，比例等于 1，所以两个距离是相等的。
• 如果是双曲线，比例大于 1

偏心率

上面讲的比例叫 "偏心率"，所以我们可以说圆锥曲线是：

如果：

• 0 <偏心率 < 1，曲线是椭圆，
• 偏心率 = 1，曲线是抛物线,
• 偏心率 > 1，曲线是双曲线。

圆的偏心率是零，所以偏心率表示曲线 "与圆有多大不同"。偏心率越大，曲线的弯度就越小。

正焦弦

正焦弦是穿过焦点而平行于准线的直线。它的长度是：

• 抛物线：四倍焦距
• 圆：直径
• 椭圆：2b²/a（a 和 b 是长轴和短轴的一半）。

 

这就是椭圆的长轴 和 短轴。

椭圆有一对焦点和准线（每边一个）。

一般方程

我们可以为这些曲线写一个方程。

因为曲线是平面曲线（虽然是从立体图形中切出来的），我们可以用笛卡尔（"x" 和 "y"）坐标。

但这些不是直线，所以只用 "x" 和 "y" 是不够的……我们要用高一级的幂：

• x² 和 y²，
• 和 x（无 y）、y（无 x），
• x 和 y 一起（xy）
• 和一个常数项.

好了，这就够了！

每项还需要个系数（A、B、C 等）……

圆锥曲线的一般方程，通用于所有圆锥曲线，是：

从这一个方程我们可以得到圆、椭圆、抛物线和双曲线……但这比较高级，容我们稍后再谈，