复数平面
 |
不,不是这个…… |
| ……这个复数平面: | 为复数而设的平面! |
(也称为“阿干特图”)
实虚得复
复数是实数与虚数的组合:
实数是我们日常用的数。
例子:12.38, ½, 0, −2000
实数的平方是正数(或零):
22 = 2 × 2 = 4
12 = 1 × 1 = 1
02 = 0 × 0 = 0
什么的平方是 −1?
?2 = −1
取−1 的平方不行,因为负负得正: (−1) × (−1) = +1。任何其他实数都不行。
所以似乎数学是缺了些什么……
……但我们可以想像一个平方是 −1 的 虚无的数。
(英语符号是字母 i,源自 “imaginary”这字,因为虚数在英语叫 “imaginary number”――“相象数”):
i2 = −1
组合起来:
复数是实数与虚数的组合
例子:3.6 + 4i、−0.02 + 1.2i、25 − 0.3i、 0 + 2i
把虚数放到平面上
你可能会熟悉实数直线:

但像这样的复数 3+4i 怎样放呢?
让我们把实数直线照常从左到右平放,然后把一条虚数直线从下到上直放:
| 我们便可以画上复数 3 + 4i
:
放在
|
||
这是 4 - 2i : 放在
|
这就是复数平面:
- 复数因为它是实与虚的组合,
- 平面因为它像个几何平面(二维)。
崭新的世界
现在我们可以把平面的概念(如笛卡儿坐标、极座标、矢量等等)应用到复数上,把我们带到一个数的崭新、更全面和更高级的世界。
复数为矢量
我们可以想像复数为矢量。

这是矢量。
它有幅度(长度和方向)。
| 这是复数 3 + 4i
以矢量表达: |
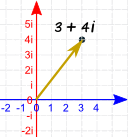 |
你亦可以把复数当作矢量加起来:
加复数 3 + 5i 和 4 − 3i :
分开来加,像这样: (3 + 5i) + (4 − 3i) = 3 + 4 + (5 − 3)i = 7 + 2i |
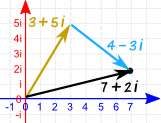 |
极型
| 再看看 3 + 4i : |  |
|
在极型它是这样: |
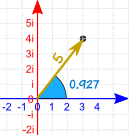 |
所以复数 3 + 4i 可以被表达为距离(5)和角度(0.927弧度)。
我们来看看怎样用笛卡儿坐标到极座标转换来把这两个复数格式互相转换:
例子:复数 3 + 4i
从3 + 4i转换:
- r = √(x2 + y2) = √(32 + 42) = √25 = 5
- θ = tan-1 (y/x) = tan-1 (4/3) = 0.927(保留3位小数)
我们得到距离(5)和角度(0.927弧度)
转和回来:
- x = r × cos( θ ) = 5 × cos( 0.927 ) = 5 × 0.6002... = 3(够准确了)
- y = r × sin( θ ) = 5 × sin( 0.927 ) = 5 × 0.7998... = 4(够准确了)
距离 5 和 角度 0.927 又转回为 3 和 4
一个通常用极型来写复数的方法是
| x + iy | = | r cos θ + i r sin θ |
| = | r(cos θ + i sin θ) |
"cos θ + i sin θ" 经常被简写为 "cis θ",所以:
x + iy = r cis θ
cis 只不过是 cos θ + i sin θ 的简写
我们可以这样写:3 + 4i = 5 cis 0.927
在某些领域,像电子, "cis" 是经常用到的!
概要
- 复数平面是一个平面,在这平面上:
- 实数从左到右排列,同时
- 虚数从下到上排列。
- 转换笛卡儿坐标为极座标:
- r = √(x2 + y2)
- θ = tan-1 ( y / x )
- 转换极座标为笛卡儿坐标:
- x = r × cos( θ )
- y = r × sin( θ )
- 极型 r cos θ + i r sin θ 经常被简写为 r cis θ
接下来……去学复数乘法。.
 。
。