矢量
这是个矢量:

矢量有量值(大小)及方向:
线的长度代表矢量的量值,而箭头指着它的方向。
把两个矢量相加就是把它们头尾连接起来:

相加(连接)的次序不重要,结果是一样的:
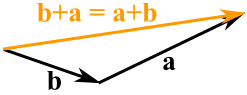
例子:飞机向北飞,风从西北吹来。
两个矢量(螺旋桨带动飞机的速度和风的速度)加起来的速度是:慢一点的地速和向北偏东的方向。
从地上看,飞机向前飞时,有一点向侧面移动。
你以前有没有看过这样的情形?例如,小鸟在逆风时好像是侧向飞行。了解矢量之后,你就会知道为什么了。
减
我们也可以用把一个矢量减去另一个矢量:
- 先把要减去的矢量倒转方向,
- 然后相加:
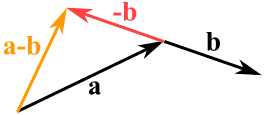
a − b
记法
矢量通常是以 粗体 字母来记录,像 a 或 b。
| 矢量也可以写成 它的头(始点)和尾(终点)的字母,上面再放个箭头,像这样: |
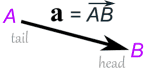 |
运算
我们怎样做矢量的运算呢?
最常用的方法是先把矢量拆分为 x部分 与 y部分,像这样:
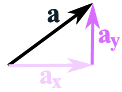
矢量 a 被分拆为
两个矢量:ax 和 ay
(我们会在 下面 解释。)
加矢量
加矢量的做法是: 加 x部分 和 加 y部分:
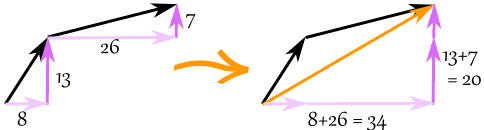
矢量 (8,13) 和 矢量 (26,7) 加起来是 矢量 (34,20)
例子:把矢量 a = (8,13) 和 b = (26,7) 相加
c = a + b
c = (8,13) + (26,7) = (8+26,13+7) = (34,20)
减矢量
先把要减去的矢量倒转,然后和另一个矢量相加。
例子:把 k = (4,5) 从 v = (12,2) 减去
a = v + −k
a = (12,2) + −(4,5) = (12,2) + (−4,−5) = (12−4,2−5) = (8,−3)
矢量的量值
矢量两旁有垂直线条代表它的量值:
|a|
也可以用双垂直线条,以免和绝对值混淆:
||a||
我们用 勾股定理 来求矢量的量值:
|a| = √( x2 + y2 )
例子:矢量 b = (6,8) 的量值是多少?
|b| = √( 62 + 82 ) = √( 36+64 ) = √100 = 10
量值为 1 的矢量称为 单位矢量。
矢量与标量
标量 只有量值 (大小)。
标量:只是一个数(像 7 或 −0.32)…… 不是矢量。
矢量 有 量值 和 方向,通常用 粗体 来写,以区别于 标量:
- 所以 c 是矢量,有量值和方向
- 但 c 只一个值,像 3 或 12.4
例子:kb 是 标量 k 乘以 矢量 b。
矢量乘以标量
把矢量乘以标量的运算是叫 "缩放" 矢量,因为这运算改变了矢量的大小。
例子:把矢量 m = (7,3) 乘以标量 3
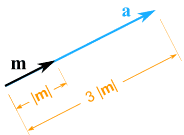 |
a = 3m = (3×7,3×3) = (21,9) |
它还是指向同一方向,但长了 3 倍
矢量乘以矢量(点积和叉积)
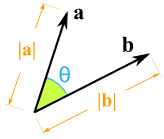 |
怎样把两个矢量相乘?有两一个方法! (阅读这些网页来了解更多。) |
多过 2维
矢量在 3维或更高也适用:
矢量 (1,4,5)
例子:把矢量 a = (3,7,4) 和 b = (2,9,11) 相加
c = a + b
c = (3,7,4) + (2,9,11) = (3+2,7+9,4+11) = (5,16,15)
例子:矢量 w = (1,−2,3) 的量值是多少?
|w| = √( 12 + (−2)2 + 32 ) = √( 1+4+9 ) = √14
以下是 4维 的例子(但画不出来!):
例子:把 (1,2,3,4) 从 (3,3,3,3) 减去
(3,3,3,3) + −(1,2,3,4)
= (3,3,3,3) + (−1,−2,−3,−4)
= (3−1,3−2,3−3,3−4)
= (2,1,0,−1)
量值与方向
我们可能知道矢量的量值和方向,但需要它的 x 和 y 长度(或相反):
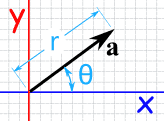 |
<=> | 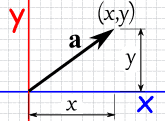 |
| 极坐标里的 矢量 a |
迪卡儿坐标里的 矢量 a |
在 极坐标和迪卡儿坐标 里你可以查阅怎样转换他们,以下是一个摘要:
| 极坐标 (r,θ) 转换为 迪卡儿坐标 (x,y) |
迪卡儿坐标 (x,y) 转换为 极坐标 (r,θ) |
|
|---|---|---|
|
|
例子
小山 和 小王在拖一个箱子。
- 小山 以 200牛顿 的力向 60°的方向拉
- 小王 以 120牛顿 的力向 45°的方向拉 (如图)
两个人的力合起来有多大,方向是什么?
我们来把两个矢量头尾连接起来:
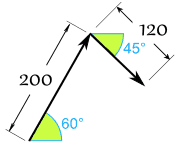
先从极坐标转换为迪卡儿坐标 (保留两位小数):
小山 的 矢量:
- x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
- y = r × sin( θ ) = 200 × sin(60°) = 200 × 0.8660 = 173.21
小王 的 矢量:
- x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0.7071 = 84.85
- y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0.7071 = −84.85
像这样:
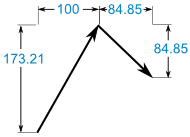
相加:
(100, 173.21) + (84.85, −84.85) = (184.85, 88.36)
这是正确的答案,不过最好把它转换回极坐标,因为问题本来是用极坐标的:
- r = √ ( x2 + y2 ) = √ ( 184.852 + 88.362 ) = 204.88
- θ = tan-1 ( y / x ) = tan-1 ( 88.36 / 184.85 ) = 25.5°
答案(舍入后)是:
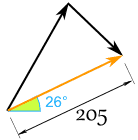
小山和小王的情形是这样的:
如果他们肩并肩地站立拉得会更有力!