叉积

矢量 有 量值（长度）和 方向：

两个矢量 可以用 "叉积 " 的方法来 "相乘"（也去看看 点积）)

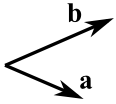
两个矢量的叉积 a × b 是与这两个矢量垂直的 矢量：

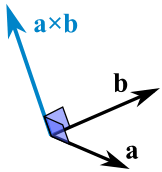
这是个 3维 现象！

运算

叉积是这样计算的：

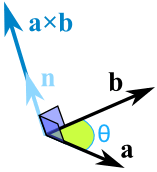
a × b = |a| |b| sin(θ) n

• |a| 是 矢量 a 的量值 （长度）
• |b| 是 矢量 b 的量值 （长度）
• θ 是 a 和 b 之间的角度
• n 是 与 a 和 b 垂直的 单位矢量

长度 是： a 的长度 乘以 b 的长度 乘以 a 和 b 之间的角的正弦

然后我们乘以矢量 n 来确保结果是指着正确的 方向 （垂直于 a 和 b）。

 

我们也可以这样计算：

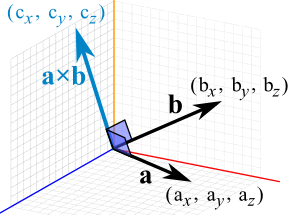
若 a 和 b 的起点是原点 (0,0,0)，叉积的终点便会在：

• c_x = a_yb_z − a_zb_y
• c_y = a_zb_x − a_xb_z
• c_z = a_xb_y − a_yb_x

 

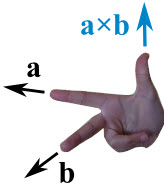
哪个方向？

若叉积指着相反的方向，它仍然是垂直于相乘的两个矢量，所以我们这样来求正确的方向：

"右手定则"

把食指指着矢量 a 的方向，把中指指着矢量 b 的方向：拇指指着的方向便是叉积的方向。

 

点积

叉积是个 矢量，也称为 矢量积。

还有一个积，叫 点积。点积是个标量 （普通的数），也称为 标量积。