常见数集
有一些常用的数有独特的名字和符号:
| 符号 | 描述 | |
|
自然数 1 及以上的整数。(在一些数学领域里是 0 及以上的整数)。去阅读更多 -> 集合是 {1,2,3,...} 或 {0,1,2,3,...} |
|
|
整数 自然数, {1,2,3,...}、负整数 {..., -3,-2,-1} 和零 {0}。所以集合是 {..., -3, -2, -1, 0, 1, 2, 3, ...} (Z 源自德语单词 "Zahlen",意思是数,因为已经用了 I 来代表虚数)。去阅读更多 -> |
|
|
有理数 等于两个整数的商的数(但不能除以零)。换句话说,分数。去阅读更多 -> Q 代表 "商"(因为已经用了 R 来代表实数)。 例子:3/2 (=1.5), 8/4 (=2), 136/100 (=1.36), -1/1000 (=-0.001) (Q 源自意大利语单词 "Quoziente",意思是两个数的商。) |
|
无理数 任何不是有理数的实数。去阅读更多 -> |
||
|
代数数 任何整系数多项式的根。 包括所有有理数和一些无理数。去阅读更多 -> |
|
超越数 任何不是代数数的数 超越数的例子包括 π 和 e。去阅读更多 -> |
||
|
实数 所有有理数和无理数,可以是整数、负数或零。 包括代数数与超越数。 去阅读实数属性 简单的想法是:数直线上任何位置的任何点(不止是整数)。 例子:1.5、-12.3、99、√2=、π 叫 "实"数因为它们不是虚数。去阅读更多 -> |
|
|
序数 平方为负数的数。 实数的平方一定是整数或零。例如 2×2=4,(-2)×(-2)=4,所以 "虚数" 好像不能存在,但其实虚数非常有用! 例子:√(-9) (=3i)、6i、-5.2i "单位"虚数是 √(-1)(负一的平方根),符号是 i 或 j。 i2 = -1 |
|
|
复数 实数与虚数的结合,格式是 a + bi,其中 a 和 b 是实数, i 是虚数。 a 和 b 可以是零,所以实数集和虚数集是复数集的子集。 例子:1 + i, 2 - 6i, -5.2i, 4 |
|
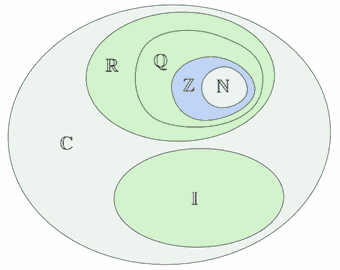 |
说明自然数是整数的子集 整数是有理数的子集 有理数是实数的子集 实数与虚数的结合是复数。 |
