向上取整与向下取整函数
向上取整/向下取整函数返回向上/向下最近的整数。(也称上取整/下取整函数)
例子:2.31 向上取整和向下取整是多少?
2.31 向下取整是 2
2.31 向上取整是 3
整数的向下取整与向上取整函数
一个整数的向下取整值和向上取整值是多少?
很容易:没改变!
例子:5 向上取整和向下取整是多少?
5 向下取整是 5
5 向上取整是 5
这是一些例子:
| x | 下取整 | 上取整 |
|---|---|---|
| −1.1 | −2 | −1 |
| 0 | 0 | 0 |
| 1.01 | 1 | 2 |
| 2.9 | 2 | 3 |
| 3 | 3 | 3 |
符号
向下取整和向上取整的符号像方括号 [ ]但没有上面或下面的部分:
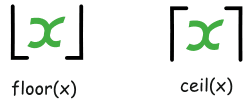
我喜欢用英语单词:floor(x) 和 ceil(x)
定义
正式定义是什么?
例子:2.31 向下取整的正式定义
结果是个整数 ……
…… 要小于(或等于) 2.31,对不?
- 2 是小于 2.31 ……
- 但 1 也是小于 2.31。
- 以下的也是:0、-1、-2、-3等等
糟了!很多整数都小于 2.31。
我们选哪个?
选最大的(即是 2)
结果是:
小于(或等于) 2.31 的最大整数是 2
所以定义是:
向下取整函数:小于或等于 x 的最大整数
向上取整也一样:
向上取整函数:大于或等于 x 的最小整数
图
向下取整是个有趣的 "阶梯"函数(像个无穷阶梯):
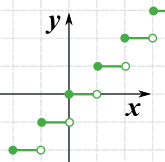
向下取整函数
(注意:实心圆点的意思是 "包括"
空心圆点的意思是 "不包括")
试试看:想象你在某个 x值(例如 x=1.5)。根据这个图, y值是多少?
例子:在 x=2,我们看到在 y=1 的空心圆点(所以不包括 x=2),也看到在 y=2 的实心圆点(包括 x=2),所以答案是 y=2
这是向上取整函数:
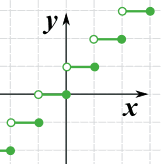
向上取整函数
"Int" 函数
"Int" 函数(英语 "integer" 的简写)和 "向下取整"函数一样,但当输入为负数时,有些计算器和电脑程序返回不同的答案:
- 有些是这样:int(−3.65) = −4(和向下取整函数一样)
- 另外一些是这样:int(−3.65) = −3(规则是:在旁边最接近零的整数,即是 "扔掉 .65")
所以要小心!
"Frac" 函数
向上取整函数 "扔掉" 分数部分。这个部分叫 "frac" 或 "分数部分"函数:
frac(x) = x − floor(x)
图像锯齿:
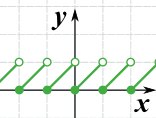
Frac 函数
例子:frac(3.65) 是什么?
frac(x) = x − floor(x)
所以:frac(3.65) = 3.65 − floor(3.65) = 3.65 − 3 = 0.65
例子:frac(−3.65) 是多少?
frac(x) = x − floor(x)
所以:frac(−3.65) = (−3.65) − floor(−3.65) = (−3.65) − (−4) = −3.65 + 4 = 0.35
但是,很多计算器和电脑程序用的公式是 frac(x) = x − int(x),所以答案也视乎 int(x) 的值是多少:
- 有些说:frac(−3.65) = 0.35,即是 −3.65 − (−4)
- 有些说: frac(−3.65) = −0.65,即是 −3.65 − (−3)
所以处理负值的 frac 函数时要小心。