可微分
可微分的意思是 导数 存在……
……并且,导数要存在于函数的 定义域 里的每一个值。
定义域定义域最简单的意思就是 |
 |
可是,来看看这个:
检测
我们可以用任何一个值 "c" 来测试,看看 极限 存在与否:
| lim h→0 |
f(c+h) − f(c) |
| h |
例子(续)
我们来计算 |x| 在 0 的极限:
| lim h→0 |
|0+h| − |0| | = | lim h→0 |
|h| − 0 | = | lim h→0 |
|h| |
| h | h | h |
极限不存在
为什么不存在?我们来看左边和右边的极限:
| 左边: | 右边: | |||||||||
|
|
两边的极限不相同,所以极限不存在。
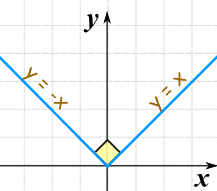
所以函数 f(x) = |x| 是不可微分的
你可以这样想:
当我们把图无穷放大,函数会不会越来越像条直线?
绝对值函数在无穷放大后还是尖锐的。
其他原因
我们来多看几个例子:
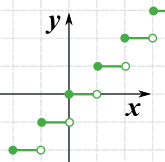 |
下取整和上取整函数 在整数是不可微分的,因为在整数值之间是不连续的,但函数对非整数是可微分的。 |
立方根函数 x(1/3) 它的导数是 (1/3)x-(2/3) (根据 幂次方法则) |
在 x=0 时,函数是未定义的,所以根本不可以问函数在那里是不是可微分的。 若函数是可微分的,它至少需要是已定义的! |
| 趋近 x = 0 时,函数越来越快地上下急剧改变,所以并不"趋近"任何一个值。 所以这函数也是不可微分的。 |
不同定义域
可是,我们可以改变定义域!
例子:函数 g(x) = |x| 在定义域 (0,+∞)
定义域是从(但不包括)0开始(所有正值)。
这个函数是可微分的。
而这也是"绝对正"确的 : )
因此,函数 g(x) = |x| 在定义域 (0,+∞) 内是可微分的。
我们也可以用其他的方法去限制定义域,从而避开 x=0 (例如所有负实数、所有非零实数等)。
为什么要这样做?
因为若一个函数是可微分的,我们便可以用微积分来处理它。
连续
若函数是可微分的,它也是 连续 的。
可微分 ⇒ 连续
但函数可以是 连续的而不是可微分的。例如绝对值函数在 x=0 是连续的。