导数入门
全是与坡度有关！
坡度 = Y 的改变X 的改变 |
 |
我们可以求两点之间的 平均 坡度.
|
 |
|
但我们怎样求在一点的坡度？ 没有什么可以测量的！ |
 |
|
但是，在导数里，我们可以用一个很小的差…… ……然后把它缩小到零。 |
 |
求个导数！
求函数 y = f(x) 的导数，我们用坡度的公式：
坡度 = Y 的改变 X 的改变 = ΔyΔx
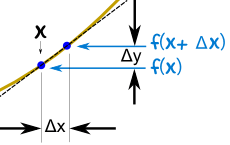
我们看到（如图）:
| x 从 | x | 变到 | x+Δx | |
| y 从 | f(x) | 变到 | f(x+Δx) |
按照这步骤去做：
- 代入这个坡度公式： ΔyΔx = f(x+Δx) − f(x)Δx
- 尽量简化
- 把 Δx 缩小到零。
像这样：
例子：函数 f(x) = x2
我们知道 f(x) = x2，也可以计算 f(x+Δx) ：
| 开始： | f(x+Δx) = (x+Δx)2 | |
| 展开 (x + Δx)2: | f(x+Δx) = x2 + 2x Δx + (Δx)2 |
| 坡度公式是： | f(x+Δx) − f(x) Δx |
| 代入 f(x+Δx) 和 f(x)： | x2 + 2x Δx + (Δx)2 − x2 Δx |
| 简化 (x2 and −x2 约去）： | 2x Δx + (Δx)2 Δx |
| 再简化（除以 Δx）： | = 2x + Δx |
| 当 Δx 趋近 0时，我们得到： | = 2x |
结果：x2 的导数是 2x
我们写 dx，而不写 "Δx 趋近 0"，所以 "的导数" 通常是写成 
x2 = 2x
"x2 的导数等于 2x"
或 "x2 的 d dx 等于 2x"
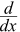x2 = 2x 的意思是什么？
意思是，对于函数 x2，在任何一点的坡度或 "变化率" 是 2x。
所以当 x=2，坡度是 2x = 4，如图所示：
或当 x=5，坡度是 2x = 10，以此类推。
注意：f’(x) 也是 "的导数" 的另一个写法：
f’(x) = 2x
"f(x) 的导数等于 2x"
再来看一个例子。
例子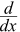：x3是什么？
我们知道 f(x) = x3，也可以计算 f(x+Δx) ：
| 开始： | f(x+Δx) = (x+Δx)3 | |
| 展开 (x + Δx)3: | f(x+Δx) = x3 + 3x2 Δx + 3x (Δx)2 + (Δx)3 |
| 坡度公式： | f(x+Δx) − f(x) Δx |
| 代入 f(x+Δx) 和d f(x)： | x3 + 3x2 Δx + 3x (Δx)2 + (Δx)3 − x3 Δx |
| 简化 （x3 and −x3 约去）： | 3x2 Δx + 3x (Δx)2 + (Δx)3 Δx |
| 再简化 （除以 Δx）： | = 3x2 + 3x Δx + (Δx)2 |
| 当 Δx 趋近 0 时，我们得到： | x3 = 3x2 |
你可以去玩玩 导数绘图器。
其他函数的导数
我们可以用同样的方法去求其他函数（如正弦、余弦、对数等等）的导数。
但在实际应用时，最常见的方法是；
但是，用这些法则时要小心！
例子：cos(x)sin(x) 的导数是什么？
你不可以把 cos(x) 的导数与 sin(x)的导数相乘来得到答案……你需要用 "乘积法则" （见 导数法则）。
答案是 cos2(x) - sin2(x)
所以你的下一步是：学习使用导数法则。
记法
"缩小到零" 可以写一个 极限，像这样：
"f 的导数等于 当 Δx 趋近零时，f(x+Δx) - f(x) 除以 Δx的极限
有时导数是写成这样的 （见 以 dy/dx 来看导数):
求导数的过程称为 "微分法"。
你用微分法……来求导数。
何去何从？
去这里学习及练习用 导数法则 来求导数。