以 dy/dx 来看导数

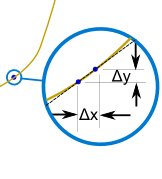
坡度 delta y / delta x

 

导数全是关于改变的……

……导数表达在任何一点的改变速度（叫变化率）。

 

在 导数入门中（请先阅读那网页！），我们探索怎样用 差 和 极限 来求导数。

在这里我们用 "dy/dx" 的记法（也称为 莱布尼茲记法) 来做。

 

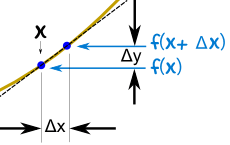
坡度 delta x and delta y

我们称函数为 "y":

y = f(x)

一、加 Δx

当 x 增大了 Δx，y 增大了 Δy

y + Δy = f(x + Δx)

从：   y + Δy = f(x + Δx)
减：   y = f(x)
结果：   y + Δy − y = f(x + Δx) − f(x)
     
简化：   Δy = f(x + Δx) − f(x)

三、变化率

求改变的速度 （叫 变化率），我们 除以 Δx：

delta y / delta x = ( f(x + delta x) - f(x) ) / delta x

 

四、把 Δx 缩小到接近于 0

我们不能把 Δx 变成 0 （因为那样便是除以 0），但我们可以使它 趋近零，称为 "dx"：

Δx 右箭头 dx

你也可以把 "dx" 视为 无穷小的。

同样，Δy 变成无穷小，我们称之为 "dy"。结果是：

dy/dx dy dx x2 a

 

用个函数来试试看

我们来试试 f(x) = x2

 

dy/dx dy dx x2 a    
  ( (x + dx)^2 - x^2 ) / dx   f(x) = x2
  ( x^2 + (2x)(dx) + (dx)^2 - x^2 ) / dx   展开 (x+dx)2
  ( (2x)(dx) + (dx)^2 ) / dx   简化 (x2-x2=0)
  2x + dx   简化分数
  2x   dx 趋近 0

 

微积分索引 极限入门