导数法则
导数 是在函数上任何一点的坡度。
有很多法则可以帮助我们去求导数。
例子：
- 常数 （像 3）的坡度永远是 0
- 直线 （像 2x 是 2，3x 是 3，以此类推）
- 等等。
以下是一些常用的法用来求函数的导数（例子在下面）。注意：这个符号 ’ 的意思是 "的导数"。.
| 常见函数 | 函数 |
导数 |
|---|---|---|
| 常数 | c | 0 |
| 直线 | x | 1 |
| ax | a | |
| 平方 | x2 | 2x |
| 平方根 | √x | (½)x-½ |
| 指数 | ex | ex |
| ax | ln(a) ax | |
| 对数 | ln(x) | 1/x |
| loga(x) | 1 / (x ln(a)) | |
| 三角 （x 的单位是 弧度） | sin(x) | cos(x) |
| cos(x) | −sin(x) | |
| tan(x) | sec2(x) | |
| 反三角 | sin-1(x) | 1/√(1−x2) |
| cos-1(x) | −1/√(1−x2) | |
| tan-1(x) | 1/(1+x2) | |
| 法则 | 函数 |
导数 |
| 乘以常数 | cf | cf’ |
| 幂次方法则 | xn | nxn−1 |
| 加法法则 | f + g | f’ + g’ |
| 减法法则 | f - g | f’ − g’ |
| 积法则 | fg | f g’ + f’ g |
| 商法则 | f/g | (f’ g − g’ f )/g2 |
| 倒数法则 | 1/f | −f’/f2 |
| 链式法则 （为 "复合函数"） |
f º g | (f’ º g) × g’ |
| 链式法则 （用 ’ ） | f(g(x)) | f’(g(x))g’(x) |
| 链式法则 （用 d dx ） | dy dx = dy du du dx | |
"的导数" 也可以写成 d dx
所以 d dx sin(x) 和 sin(x)’ 是 一样的，只不过写法不同
举例
例子：sin(x) 的导数是什么？
从上面的列表我们可以看到答案是 cos(x)
可以写为：
sin(x) = cos(x)
或：
sin(x)’ = cos(x)
幂次方法则
例子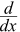：x3 是什么？
问题是 "x3 的导数是什么？"
我们可以用幂次方法则，以 n=3:
xn = nxn−1
x3 = 3x3−1 = 3x2
例子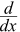：(1/x) 是什么？
1/x 等于 x-1
我们可以用幂次方法则，以 n = −1:
xn = nxn−1
x−1 = −1x−1−1 = −x−2
乘以常数
例子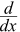：5x3 是什么？
cf 的导数 = cf’
5f 的导数 = 5f’
幂次方法则：
x3 = 3x3−1 = 3x2
所以：
5x3 = 5x3 = 5 × 3x2 = 15x2
加法法则
例子：x2+x3 的导数是什么？
加法法则说：
f + g 的导数 = f’ + g’
所以我们可以求每项的导数，然后求它们的和。
幂次方法则：
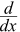- x2 = 2x
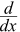- x3 = 3x2
所以：
x2 + x3 的导数 = 2x + 3x2
减法法则
变量不一定是 x，我们可以相对于 v 来求导数：
例子：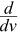
(v3−v4) 的导数是什么？
减法法则说：
f − g 的导数 = f’ − g’
所以我们可以求每项的导数，然后求它们的差。
幂次方法则：
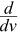- v3 = 3v2
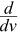- v4 = 4v3
所以：
v3 − v4 的导数 = 3v2 − 4v3
加法、减法、乘以常数和幂次方法则
例子：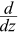
(5z2 + z3 − 7z4) 的导数是什么？
幂次方法则：
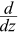- z2 = 2z
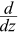- z3 = 3z2
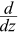- z4 = 4z3
所以：
(5z2 + z3 − 7z4) = 5 × 2z + 3z2 − 7 × 4z3 = 10z + 3z2 − 28z3
积法则
例子：cos(x)sin(x) 的导数是什么？
积法则说：
fg 的导数是 = f g’ + f’ g
在这个例子里：
- f = cos
- g = sin
根据上面的列表：
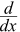- cos(x) = −sin(x)
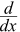- sin(x) = cos(x)
所以：
cos(x)sin(x) 的导数 = cos(x)cos(x) − sin(x)sin(x)
= cos2(x) − sin2(x)
倒数法则
例子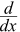：(1/x) 的导数是什么？
倒数法则说：
1/f 的导数 = −f’/f2
若 f(x)= x，f’(x) = 1
所以：
1/x 的导数是 = −1/x2
结果和在上面用幂次方法则求的一样。
链式法则
例子： d dx sin(x2) 的导数是什么？
sin(x2) 是由 sin() 和 x2 结合而成：
- f(g) = sin(g)
- g(x) = x2
链式法则说：
f(g(x)) 的导数 = f'(g(x))g'(x)
导数分别是：
- f'(g) = cos(g)
- g'(x) = 2x
所以：
d dx sin(x2) = cos(g(x)) (2x)
= 2x cos(x2)
链式法则也可以写成： dy dx = dy du du dx
让我们用这个公式来再做一遍上面的例子：
例子： d dx sin(x2) 的导数是什么？
dy dx = dy du du dx
设 u = x2，所以 y = sin(u)：
d dx sin(x2) = d du sin(u) d dx x2
分别微分：
d dx sin(x2) = cos(u) (2x)
代入 u = x2 和简化：
d dx sin(x2) = 2x cos(x2)
结果和上面一样！
再来看看一些链式法则的例子：
例子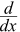：(1/cos(x)) 的导数是什么？
1/cos(x) 是由 1/g 和 cos() 结合而成：
- f(g) = 1/g
- g(x) = cos(x)
链式法则说：
f(g(x)) 的导数 = f’(g(x))g’(x)
导数分别是：
- f'(g) = −1/(g2)
- g'(x) = −sin(x)
所以：
(1/cos(x))’ = −1/(g(x))2 × −sin(x)
= sin(x)/cos2(x)
注意：sin(x)/cos2(x) 也是 tan(x)/cos(x)，或其他不同的形式。
例子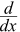：(5x−2)3 的导数是什么？
链式法则说：
f(g(x)) 的导数 = f’(g(x))g’(x)
(5x-2)3 是由 g3 和 5x-2 结合而成：
- f(g) = g3
- g(x) = 5x−2
导数分别是：
- f'(g) = 3g2 （用幂次方法则）
- g'(x) = 5
所以：
(5x−2)3 = 3g(x)2 × 5 = 15(5x−2)2