数学模型
数学可以用来为现实世界"建立模型",亦既是模拟现实世界里的事物或情形。
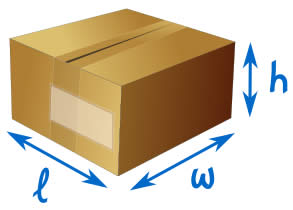
这便是箱子里的空间的一个(非常简单的)数学模型。
准确吗?
模型和现实是不一样的。
在这例子里,我们忽略了纸壳的厚度和很多其他"实在"的东西。
但我们希望这模型是足够好和够用的。
 |
若我们需要以箱子的大少来付邮费,我们可以量度一下来计算应付多少钱. 我们也可用来决定要买哪个箱子. 所以这模型是有用的! |
可是,我们可能需要更加精确。若我们可能每天要邮寄成千上万的箱子,我们便要考虑到纸壳的厚度了。所以我们现在来改善这模型:
纸壳的厚度是 "t",所有尺寸都是在箱子的外面量度的……箱子里面的空间有多大?
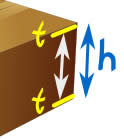 |
我们需要缩短箱子里面的尺寸,除去纸壳的厚度:
公式变成: 内部体积 = (l-2t) × (w-2t) × (h-2t)
|
我们现在有一个比较好的模型。还不够完美(可能浪费了空间,因为里面的物件放得不好,等等……),但模型是改善了。
故此,模型不是现实,但要足够好才有用。
思考模型
有了模型后,我们可以用它来做很多:
例子:你公司用 200x300x400 mm 大小的箱子,纸壳厚度是 5mm。
有人提议用 4mm 厚的纸壳……这会比现在好多少?
我们来比较目前和新的体积:
- 目前体积 = (200-2×5) × (300-2×5) × (400-2×5) = 21,489,000 mm3
- 新体积 = (200-2×4) × (300-2×4) × (400-2×4) = 21,977,088 mm3
改变是:
(21,977,088-21,489,000)/21,489,000 ≈ 多了 2% 体积
所以模型是有用的――我们用它来知道箱子里的空间会增加 2%(若外面的尺寸相同)。
但我们可能还要考虑其他的"现实"条件,例如,"箱子够坚固吗?"
清晰思维
我们需要清晰的思维来建立一个数学模型!
例子:在这小区狗的数目是猫的两倍。我们怎样把这写成方程式?
- 以 D = 狗的数目
- 以 C = 猫的数目
好了,方程是: 2D = C
还是: D = 2C
仔细想想!
正确的答案是 D = 2C
(2D = C 是常见的错误)
再来一个:
例子:你是八小时工作班的监工。最近员工的休息时间缩短了10分钟,但产量没有增加。
乍看没有什么好模拟的,产量都没有增加。
慢着……员工工作时间长了10分钟,但产量没变,所以每小时生产率一定下降了!
假设员工以前工作 7 小时(420分钟):
每小时生产率的改变 = 410/420 = 0.976……
这是下降了超过 2%
更糟的是:休息时间不会影响到工作班的头几个小时,所以在以后的几小时,生产率可能下降了 4 或 5%。
你可以提议:
- 详细分析工作班里每一小时的生产率
- 尝试不同的休息时间来试验对生产率的影响
复杂的例子:最经济的尺寸
好,我们来建立数学模型去解决一个现实问题。
你的公司要自己造箱子!
管理层决定了每个箱子要放 0.02m3 (0.02 立方米,等于 20公升) 体积的螺丝。
箱子要有正方形的底,和双倍厚度的顶和底。
纸壳的价钱是每平方米 ¥0.30。
你负责去决定最经济的箱子尺寸。
第一步:画个草图!
画草图会很有用!
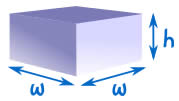 |
底是正方形,所以我们就以 "w" 为长度和宽度 |
箱子有 4 边和双倍厚度的顶和底。 可以切出这样形状的纸壳来造箱子(现实可能更复杂): |
第二部:列出公式。
在这模型里我们不考虑厚度:
体积 = w × w × h = w2h
体积应该是 0.02m3:
w2h = 0.02
面积:
4边的面积 = 4 × w × h = 4wh
双倍厚度的顶和底的面积 = 4 × w × w = 4w2
总共需要的纸壳:
纸壳的面积 = 4wh + 4w2
第三步:列出成本的公式
我们想要成本的公式:
成本 = ¥0.30 × 纸壳的面积
= ¥0.30 × (4wh + 4w2)
若知道宽度 和 高度,便可以计算成本
可是这有点不好使……二元函数。
但这还可以简化!因为宽度和高度都是和体积有联系的:
体积 = w2h = 0.02
……可以重排为……
h = 0.02/w2
……代入成本公式……
成本= ¥0.30 × (4w×0.02/w2 + 4w2)
现在成本只是与宽度有关联了。
再简化:
成本= ¥0.30 × (0.08/w+ 4w2)
第四步:画图来找最低成本
画什么图?公式只在宽度大于零时是才有意义(那还用说!?),同时当宽度大于 0.5m,成本便不断增加。
这是成本公式的图,当宽度在 0.0 m 和 0.55 m之间:
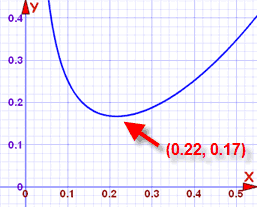
y= 0.3(0.08/x+4x2)的图
x 是宽度, y 是成本
一看就知道成本在大约 (0.22, 0.17) 最低。换句话说:
- 当宽度是大约 0.22 m(x值),
- 每个箱子的最低成本你是大约 ¥0.17(y值)。
实际上,这幅图告诉我们宽度在大约 0.20 和 0.24 之间时,最低成本都不会有大的改变。
第五步:建议
基于这数学模型,你可以建议:
- 宽度 = 0.22 m
- 高度 = 0.02/w2 = 0.02/0.222 = 0.413 m
- 成本 = ¥0.30 × (0.08/w+ 4w2) = ¥0.30 × (0.08/0.22+ 4×0.222) = ¥0.167
每个箱子大约 16.7 分
任何在 0.20 m 和 0.24 m 之间的宽度都可以。
你也可有以下提议来改善这模型:
- 加入 胶/卡钉 和 组装 的成本
- 加入 切纸壳时的损耗
- 这箱子的形状大小方便包装、处理和储藏吗?
- 你自己的主意!
预测未来
数学模型也可以用来预测未来。
例子:冰激凌公司记录下每天卖了多少冰激凌。
 |
它们用不同日子的销售额与当天的天气来建立一个销售额与天气的数学模型。 这模型可以用天气预报来预测销售额,从而预先决定冰激凌的生产量! |
计算机模拟
数学模型可以非常复杂,所以人们时常把模型写成计算机程序,使其成为一个计算机模型。
例子包括:
- 天气预测
- 经济模型(预测利率、失业率等等)
- 模拟大型建筑物在应力下的反应(桥、摩天大厦等等)
- 还有很多……
若你是这方面的专家,你就一辈子不愁吃穿了!