解应用题
这网页有很多例子!
在代数里我们时常见到应用题,例如:
例子:小王和大牛是网球运动员。
上周末小王比大牛多打了4局,他们总共打了12局。
大牛打了多少局?
我们怎样去答这个问题?
一个技巧是把问题分成两个部分:
把语文转为代数。
用代数来解。
把语文转为代数。
按以下步骤把问题从语文转为代数的语言
- 先把问题从头到尾看一遍
- 如有必要,画个草图
- 以英语字母代替每个值
- 找出合适的公式
我们也应该写下问题问的究竟是什么,这会给我们一个目标!
也需要留意关键词:
| 如果见到 | 想 | |
|---|---|---|
加、总、和、增加、更多、合、一起、还有、多于 |
+ | |
减、少、差、更少、减少、缩小 |
− | |
乘、次、积、因数 |
× | |
除、商、每、分之、比、百分比、率 |
÷ | |
| 使……最大 或 使……最小 | 几何 公式 |
|
| 率、速率 | 距离 公式 |
|
| 多久、日/天、小时、分、秒 | 时间 |
清晰的思维
有时候问题的措词会有点复杂,可能使你理解错误,例如:
例子:在这个小区狗的数目是猫的两倍。我们怎样把这写成方程式?
- 设 D = 狗的数目
- 设 C = 猫的数目
好了,方程是:2D = C
还是:D = 2C
仔细想想!
正确的答案是 D = 2C
(2D = C 是常见的错误)
例子: 小王的书比大牛少两本。我们怎样把这写为一个方程?
- 设 S = 小王的书的数量
- 设 A = 大牛的书的数量
方程是:S − 2 = A
还是:S = A − 2
还是:S = 2 − A
正确的答案是: S = A − 2
例子
我们先来看看一个非常简单的例子:
例子:一个矩形的花园是 12m 长,5m 宽,它的面积是多少?
把语文转为代数:
草图:
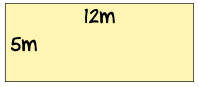
字母:
- 设 w 为矩形的宽度:w = 12m
- 设 h 为矩形的高度:h = 5m
矩形的面积 的公式是:A = w × h
我们需要求面积。
解:
A = w × h = 12 × 5 = 60 m2
面积是 60 平方米。
现在我们尝试去解在页顶的例子:

例子:小王和大牛是网球运动员。上周末小王比大牛多打了4局,他们总共打了12局。大牛打了多少局?
把语文转为代数:
字母:
- 设 S 为小王打的局数
- 设 A 为大牛打的局数
我们知道小王比大牛多打了4局,所以:S = A + 4
我们也知道他们总共打了12局:S + A = 12
我们想求大牛打了多少局:A
解:
| 开始: | S + A = 12 | |
| S = A + 4,所以我们可以 把 "A + 4" 代入 S: |
(A + 4) + A = 12 | |
| 简化: | 2A + 4 = 12 | |
| 每边减 4: | 2A = 12 − 4 | |
| 简化: | 2A = 8 | |
| 每边除以 2: | A = 4 |
大牛打了4局网球。
检验:小王比大牛多打了4局,所以小王打了8局。 他们总共打了 8 + 4 = 12局。对了!
比较复杂的例子:

例子:大牛和小王都造桌子。
在12天里,他们一起造了10张桌子。
大牛自己一个人可以在30天里造10张桌子。
小王造10张桌子要几天?
把语文转为代数:
字母:
- 设 a 为 大牛 每天造的桌子的数量
- 设 s 为 小王 每天造的桌子的数量
12天里,大牛和小王一共造了10张桌子,所以:12a + 12s = 10
30天里,大牛 自己可以造10张:30a = 10
我们想求小王造10张桌子要多久。
解:
30a = 10所以大牛每天可以造:a = 10/30 = 1/3 张桌子
| 开始: | 12a + 12s = 10 | |
| 把 "1/3" 代入 a: | 12(1/3) + 12s = 10 | |
| 简化: | 4 + 12s = 10 | |
| 每边减 4: | 12s = 6 | |
| 每边除以 12: | s = 6/12 | |
| 简化: | s = 1/2 |
就是说,小王每天可以造半张桌子(比大牛快!)
所以小王在20天里可以造10张桌子。
我认为小王的工资也应该高一点。
我们再来看一个"代"数的例子:

例子:珍珍在锻炼去参加全运会。
她的锻炼计划是每星期有几天练5个小时,其他的日子练3个小时。
在一个星期的7天里,她总共练了27个小时。她有几天练了5个小时?
字母:
- 练 "5个小时" 的日数:d
- 练 "3个小时" 的日数:e
一星期有7天,所以:d + e = 7
珍珍一星期练27小时,d天练5个小时,e天练3个小时:5d + 3e = 27
我们想求她有几天练5个小时:d
解:
| d + e = 7 | ||
| 所以: | e = 7 − d | |
| 代入 5d + 3e = 27 | 5d + 3(7−d) = 27 | |
| 简化: | 5d + 21 − 3d = 27 | |
| 每边减 21: | 5d − 3d = 6 | |
| 简化: | 2d = 6 | |
| 每边除以 2: | d = 3 |
珍珍每星期有 "3" 天练5个小时
检验:3天练5个小时,所以 4(=7−3)天练3个小时。
3 × 5 小时 = 15 小时,加 4 × 3 小时 = 12 小时,一共 27 小时
几何例子:
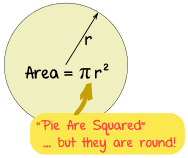
例子:圆形 的面积是 12 mm2,半径是多长?
字母:
- 设 A 为 面积:A = 12 mm2
- 设 r 为 半径
面积的公式是:A = π r2
我们想求 半径。
解:
我们需要重排这个公式
| 开始: | A = π r2 | |
| 换边: | π r2 = A | |
| 每边除以 π: | r2 = A / π | |
| 每边去平方根: | r = √(A / π) | |
| 可以把面积的值代入公式: | r = √(12 / π) | |
| 结果是: | r = 1.954 (保留三位小数) |
例子:A 立方体 的体积是 125 mm3,他的表面积是多大?
画个草图:

字母:
- 设 V 为 体积
- 设 A 为 表面积
- 设 s 为 立方体的边长
公式:
- 立方体的体积:V = s3
- 立方体表面积:A = 6s2
我们想求表面积。
解:
先用体积的公式来求 s:
| 开始: | V = s3 | |
| 换边: | s3 = V | |
| 取每边的立方根: | s = ∛(V) | |
| 代入体积的值: | s = ∛(125) = 5 |
现在来求表面积:
| 开始: | A = 6s2 | |
| 代入 s 的值: | A = 6(5)2 | |
| A = 6 × 25 = 150 mm2 |
与钱有关的例子:

例子:祖儿在薄饼店打工。她的超时工资是正常工资的 1¼ 倍。
上星期祖儿做了40小时的正常工作及12小时的超时工作。如果祖儿上星期的工资是$660,她每小时的正常工资是多少?
字母:
- 祖儿的正常工资:每小时 $N
公式:
- 40小时,每小时 $N = $40N
- 超时工资是正常工资的 1¼ 倍 = 每小时 $1.25N
- 12小时,每小时 $1.25N = $(12 × 1¼N) = $15N
- 她总共赚了 $660,所以:
$40N + $(12 × 1¼N) = $660
我们想求祖儿的正常工资 $N。
解:
| 开始: | $40N + $(12 × 1¼N) = $660 | |
| 简化: | $40N + $15N = $660 | |
| 再简化: | $55N = $660 | |
| 每边除以 55: | $N = $12 |
祖儿的正常工资是每小时 $12
检验
祖儿的正常工资是每小时 $12,所以她的超时工资是每小时 1¼ × $12 = 每小时$15。她的正常工资是 40 × $12 = $480,超时工资是 12 × $15 = $180,总共是 $660
再来一些关于钱的例子,以下两个例子都与复利有关
例子:大牛把 $2000 存进银行,年复利率是 11%。三年后存款是多少?
这是复利的公式:
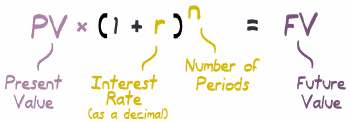
我们用这些字母:
- 现值 PV = $2,000
- 利率 (分数):r = 0.11
- 期数:n = 3
- 终值 (我们求的值):FV
我们相求终值:FV
解:
| 开始: | FV = PV × (1+r)n | |
| 代入已知值: | FV = $2000 × (1+0.11)3 | |
| 计算: | FV = $2000 × 1.367631 | |
| 计算: | FV = $2735.26 (至最接近的分) |
例子:小李把 $1,000 存进储蓄账户。利息是固定利率的复利。九年后小李的存款是 $1,551.33
储蓄账户的年利率是多少?
这是 复利 公式:
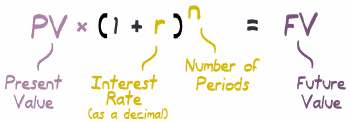
我们用这些字母:
- 现值 PV = $1,000
- 利率 (我们求的值):r
- 期数:n = 9
- 终值:FV = $1,551.33
我们想求利率:r
解:
| 开始: | FV = PV × (1+r)n | |
| 代入已知值: | $1,551.33 = $1000 × (1+r)9 | |
| 换边: | $1000 × (1+r)9 = $1,551.33 | |
| 每边除以 1000: | (1+r)9 = $1,551.33 / $1,000 | |
| 简化: | (1+r)9 = 1.55133 | |
| 9次根: | 1+r = 1.55133(1/9) | |
| 计算: | 1+r = 1.05 | |
| 计算: | r = 0.05 = 5% |
年利率是 5%
检验: $1,000 × (1.05)9 = $1,000 × 1.55133 = $1,551.33
关于比 的问题:
例子:在年初,班上男孩和女孩的比是 2 :1
现在,半年后,四个男孩退学了,并且新来了两个女孩。男孩和女孩的比变成了 4 :3
班上总共有几个小孩?
字母:
- 现在男孩的数目:b
- 现在女孩的数目:g
现在的比是 4 :3
| b | = | 4 |
| g | 3 |
这可以重排为 3b = 4g
在年初有 (b + 4) 个男孩和 (g − 2) 个女孩,比是 2 :1
| b + 4 | = | 2 |
| g − 2 | 1 |
这可以重排为 b + 4 = 2(g − 2)
我们想求现在总共有几个小孩:b + g
解:
| 开始: | b + 4 = 2(g − 2) | |
| 简化: | b + 4 = 2g − 4 | |
| 每边减 4: | b = 2g − 8 | |
| 每边乘以 3 (来得到 3b): | 3b = 6g − 24 | |
| 把 4g 代入 3b: | 4g = 6g − 24 | |
| 每边减 6g: | −2g = − 24 | |
| 每边除以 −2: | g = 12 |
有 12 个女孩!
3b = 4g,因此 b = 4g/3 = 4 × 12 / 3 = 16,所以有 16 个男孩
现在班上 12个女孩和 16个男孩,一共有 28个小孩。
检验
现在有 16个男孩和 12个女孩,所以男孩和女孩的比是 16 :12 = 4:3
在年初有 20个男孩和 10个女孩,所以比是 20 :10 = 2 :1
在下面的例子里,我们需要解 二次方程:
例子:两个连续的偶整数的积是 168。求它们的值。
连续 的意思是一个和后面顺序的一个。它们是 偶数,所以可以是 2 和 4 或 4 和 6 等等。
设 n 为小的整数,大的整数便一定是 n+2
它们的积(相乘的结果)是 168,所以:
n(n + 2) = 168
我们想求这两个整数
解:
| 开始: | n(n + 2) = 168 | |
| 展开: | n2 + 2n = 168 | |
| 每边减 168: | n2 + 2n − 168 = 0 |
这是个 二次方程,有很多方法去解它。用 二次方程式解算器,我们得到的答案是 −14 和 12。
检验 −14: −14(−14 + 2) = (−14)×(−12) = 168 正确
检验 12: 12(12 + 2) = 12×14 = 168 正确
有两个答案:−14、−12 和 12、14。
注意:我们也可以用 "猜测和检测" 的方法来做:
- 试试 n=10: 10(12) = 120 错误 (太小)
- 再试 n=12: 12(14) = 168 正确
可是,若我们忘了 负负得正,我们便可能忽略了 (−14)×(−12) 这个答案。
最后一个例子:
例子:你是建筑师。你的客户想要一个长度为宽度两倍的房间,并且沿这房间长的一边有个3米宽的
阳台。
客户给你 56 平方米的大理石磁砖来为房间和阳台铺地。
房间的长度是多少?
先来画个草图!:
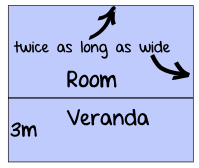
字母:
- 房间的长度:L
- 房间的宽度:W
- 房间和阳台的面积:A
已知:
- 房间宽度是长度的一半:W = ½L
- 总面积是(宽度 + 3)乘以长度:A = (W+3) × L = 56
我们想求房间的长度:L
解:
| 开始: | (W + 3) × L = 56 | |
| 代入 W = ½L:: | (½L + 3) × L = 56 | |
| 简化: | ½L2 + 3L = 56 | |
| 所有项乘以 2: | L2 + 6L = 112 | |
| 每边减 112:: | L2 + 6L − 112 = 0 |
这是个 二次方程,有很多方法来解它,这里我们用 因式分解:
| 开始: | L2 + 6L − 112 = 0 | |
| 找两个积是 ac=−112 并且 和是 b=6 的数:14 和 −8: |
L2 + 14L − 8L − 112 = 0 | |
| 合并: | L(L +14) − 8(L + 14) = 0 | |
| 合并: | (L − 8)(L + 14) = 0 |
结果是 L = 8 或 −14
二次方程有两个答案,但只有一个是正确的答案,因为房间的长度不能是负数!
因此,房间的长度是 8 m
检测
L = 8,所以 W = ½L = 4
S矩形的面积 = (W+3) × L = 7 × 8 = 56
好了……
……希望这些例子可以帮你领略怎样去解应用题。现在我建议你去练习一下……学以致用,熟能生巧!