余式定理
与
因式定理
或:怎样去避免在因式分解中做多项式长除
你记得在算术里做除法吗?
"7 除以 2 等于 3 余 1"
除法里每一部分都有个名字:
这可以 重写 为一个和,像这样:
多项式
我们也可以 除多项式。
f(x) ÷ g(x) = q(x) 余 r(x)
但以和的形式写出来比较好:
就像这个用 多项式长除 的例子:
例子:2x2-5x-1 除以 x-3
- f(x) 是 2x2-5x-1
- g(x) 是 x-3
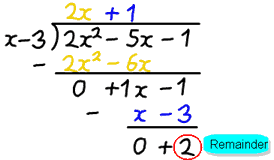
做完后我们得到的答案是 2x+1,但剩下 2为余项。
- q(x) 是 2x+1
- r(x) 是 2
用 f(x) = g(x)·q(x) + r(x) 的格式,我们写成:
2x2-5x-1 = (x-3)(2x+1) + 2
你还要知道:
当除以一次多项式(例如 "x-3")时,余项的 次数是 0 (就是一个常数,像 "4")。
我们在余式定理也会用到这概念:
余式定理
把多项式f(x) 除以 x-c 的结果是:
f(x) = (x-c)·q(x) + r(x)
但 r(x) 只不过是个常数 r (我们在上面讲过:除以 (x-c) 的余项是个常数)。我们现在可以写成:
f(x) = (x-c)·q(x) + r
把 c 代入 x:
f(c) = (c-c)·q(c) + r
f(c) = (0)·q(c) + r
f(c) = r
这便是
余式定理:
多项式 f(x) 除以 x-c 的余项 r 是 f(c)
故此,求除以 x-c 的余项,我们不用做除法:
我们只需要求 f(c)。
应用:
例子:2x2-5x-1 除以 x-3
(续上)
不需要除以 (x-3)……求 f(3) 就行了:
2(3)2-5(3)-1 = 2x9-5x3-1 = 18-15-1 = 2
这和我们在上面做除法时所得到的余项是一样的。
我们不需要做长除!
例子:除以 x-4
(续上)
除以 "x-4" 的余项是多少?
"c" 是 4,所以我我们求 f(4):
2(4)2-5(4)-1 = 2x16-5x4-1 = 32-20-1 = 11
我们不需要做长除来求余项。
因式定理
接下来……
若 f(c) 是 0 呢??
……这就是说 余项是 0……故此
……(x-c) 一定是多项式的因式!
例子:x2-3x-4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0
所以 (x-4) 是 x2-3x-4 的因式
这就是
因式定理:
若 f(c)=0,则 x-c 是多项式的因式
反之亦然:
若 x-c 是多项式的因式,则 f(c)=0
有用吗?
知道 x-c 是因式便是知道 c 是多项式的一个根(反之亦然)。
"x-c" 为因式 与 "c" 为根 的意思是相同的
知道一个就是知道另外一个
我们可以用这个定理来检验 (x-c) 是否一个多项式的因式
例子:2x3-x2-7x+2
这是个三次多项式,要解它会很困难。我们先来画个图:
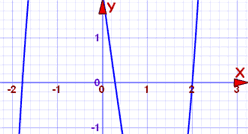
线在三个地方经过 x轴,其中一点可能在 x=2。检测很简单:
f(2) = 2(2)3-(2)2-7(2)+2 = 16-4-14+2 = 0
对了!f(2)=0,所以我们找到一个根 和 一个因式。
故此 (x-2) 是 2x3-x2-7x+2 的因式
线好像在 -1.8 也经过 x轴,那么(x+1.8)是不是因式?
f(-1.8) = 2(-1.8)3-(-1.8)2-7(-1.8)+2 = -11.664-3.24+12.6+2 = -0.304
不是。 (x+1.8) 不是因式。
总结
余式定理:
- 多项式 f(x) 除以 x-c 的余项是 f(c)
因式定理:
- 若 f(c)=0,则 x-c 是多项式的因式
- 若 x-c 是多项式的因式,则 f(c)=0


