线性方程组
线性方程 是 直线 的 方程。
方程组 是一组有 两个或以上有关联的方程。
举个例:
例子:你和马赛跑

赛跑!
你一分钟可以跑 0.2 km
马一分钟可以跑 0.5 km。但给马加鞍要花 6 分钟。
在马赶上你之前你可以跑多远?
我们可以制定 两个方程(d=距离(千米),t=时间(分钟)):
| 你: | d = 0.2t | |
| 马: | d = 0.5(t−6) |
我们有一个方程组,方程是线性方程:
好像 10 分钟后马赶上你了……你只跑了 2 千米。
下次跑快点。
你现在知道线性方程组是什么了。
我们再来多了解一点……
求解
线性方程的形式不一定是这样的:y = 3x+2,
它也可能是这样的: y − 3x = 2
或者这样:−3x + y = 2
以上全是同一个线性方程
也可以有很多方法去解线性方程!
再举个例:
例子:解这两个方程:
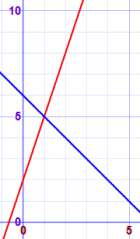
- x + y = 6
- −3x + y = 2
这是这两个方程的图:
我们的目标是找到这两条线在哪里相交。
对,用眼可以看得到,但这里我们用代数来解!
我们怎样解?有很多方法!在这个例子里,两个方程都有 "y" 这项,所以我们可以试试用第一个方程减第二个方程:
简化成:
x=1 是在两条线上。
用其中一个方程来求在 x=1 时 y 的值(在这一点 y 的值是一样的)。这里我们用第一个方程(你可以自己用第二个方程来试试):
解是:
x = 1 和 y = 5
在图上看到的也是这样!
线性方程
| 线性方程 可以使 2 维的…… (例如 x 和 y) |
 |
|
 |
……或 3 维 (例如 x、y 和 z)…… |
|
| ……或 4 维……甚至更高! |
(但不能画出来) |
线性方程只能有简单的变量。不能有 x2、y3、√x 等等:
线形与非线性
公共变量
若要方程组里的方程 "互相有关联",方程便要有公共变量:
方程组有两个或以上的方程和一个或以上的变量
很多变量
方程组可以有很多方程和很多变量。
例子:3 个方程,3 个变量
| 2x | + | y | − | 2z | = | 3 |
| x | − | y | − | z | = | 0 |
| x | + | y | + | 3z | = | 12 |
可以有任何组合:
- 2 个方程,3 个变量,
- 6 个方程,4 个变量,
- 9,000 个方程,567 个变量,
- 等等
解
若方程的个数等于变量的个数,则方程组很可能有解,不一定有,但很可能。
只有三个可能:
- 无(零)解
- 一个解
- 无穷多个解
若无解,方程便是"不相容"方程。
若有一个或无穷多个解,方程便是"相容"方程
这是2 个方程,2 个变量的图:
独立
"独立" 的意思是每个方程都含有新信息。
否则方程便是"相关"的。
也叫"线性独立" 和 "线性相关"
例子:
- x + y = 3
- 2x + 2y = 6
这些方程是 "相关"的,因为它们其实是同一个方程,第二个是第一个乘以 2。
所以第二个方程没有新信息。
方程在哪里为真
我们需要解的是在什么地方全部的方程都同时为真。
为真是什么意思?
例子:你与马
在"你"的方程的线上的每一点,方程都为真(但在任何其他地方都不为真)。
在那条线上的任何一点,d 都是等于 0.2t
- 在 t=5 和 d=1,方程是 对 的 (d = 0.2t 吗?是,1 = 0.2×5 是对的)
- 在 t=5 和 d=3,方程是 不对 的 (d = 0.2t 吗?不,3 = 0.2×5 是不对的)
同样,在"马"的方程的线上的每一点,方程都为真(但在任何其他地方都不为真)。
但是,只有在两条线的交叉点(t=10,d=2),两个方程都为真。
两个方程需要同时为真……
。。。。。线性方程组的另一个名字是 "联立线性方程"
用代数来解
我们可以不用图,而用代数来解:
例子:你与马
我们用代数来解它。
方程组是:
- d = 0.2t
- d = 0.5(t-6)
在这例子,把方程放在一起比较简单:
d = 0.2t = 0.5(t-6)
| 展开 0.5(t-6): | 0.2t = 0.5t - 3 | |
| 每边减 0.5t: | -0.3t = -3 | |
| 每边除以 -0.3: | t = -3/-0.3 = 10分钟 | |
知道你在什么时候被马赶上了! |
||
| 知道 t,我们便可以求 d: | d = 0.2t = 0.2×10 = 2 km | |
答案是:
t = 10分钟 , d = 2 km
代数与图
为什么要用代数,用图不是更容易吗?因为:
一个简单的图不能用来解多于 2 个变量的方程组。
有两个常用的代数方法来解方程组:
- 代入法
- 消元法
我们会用2个变量和3个变量为例来解释每一个方法……
代入法
步骤是:
- 把一个方程写成 "变量 = ……" 的形式
- 在其他的方程中替代(代入)那个变量。
- 解其他的方程
- (如有需要,重复以上步骤)
2 个方程,2 个变量 的例子:
例子:
- 3x + 2y = 19
- x + y = 8
我们可以从 任何方程 和 任何变量开始。
这里我们用第二个方程和变量 "y"(第二个方程比较简单)。
把第二个方程写成 "变量 = ……" 的形式:
把 x 从 x + y = 8 的每边减去,得到 y = 8 - x。方程变为:
- 3x + 2y = 19
- y = 8 - x
把 "8 - x" 代入第一个方程的 "y" 里:
- 3x + 2(8 - x) = 19
- y = 8 - x
用一般的代数解法来解:
展开 2(8-x):
- 3x + 16 - 2x = 19
- y = 8 - x
减 3x-2x = x:
- x + 16 = 19
- y = 8 - x
最后 19-16=3
- x = 3
- y = 8 - x
知道 x了,把它代入 y = 8 - x:
- x = 3
- y = 8 - 3 = 5
答案是:
x = 3 和 y = 5
注意:因为有一个解,方程是 "相容"的
检验:你自己来计算,看看代入 x = 3 和 y = 5 后,两个方程是不是对的?
代入法:3 个方程,3 个变量
好了,现在来一个长一点的例子:3 个方程,3 个变量。
这其实不难,不过要多花点时间!
例子:
- x + z = 6
- z - 3y = 7
- 2x + y + 3z = 15
我们先把变量排列好,这样比较不容易犯错:
| x | + | z | = | 6 | |||||
| - | 3y | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 |
我们可以从 任何方程 和 任何变量开始。这里我们用第一个方程和变量 "x"。
把第一个方程写成 "变量 = ……"的形式:
| x | = | 6 - z | |||||||
| - | 3y | + | z | = | 7 | ||||
| 2x | + | y | + | 3z | = | 15 | |||
把 "6 - z" 代入第三个方程的 "x" 里:
(只有第三个方程有变量 x )
| x | = | 6 - z | ||||||||
| - | 3y | + | z | = | 7 | |||||
| 2(6-z) | + | y | + | 3z | = | 15 | ||||
用一般的代数解法来解:
2(6-z) + y + 3z = 15 简化成 y + z = 3:
| x | = | 6 - z | |||||||
| - | 3y | + | z | = | 7 | ||||
| y | + | z | = | 3 | |||||
有进步,但还没做完。
重复以上的步骤,但用最后的两个方程。
把一个方程写成 "变量 = ……" 的形式:
我们用最后的方程和变量 z:
| x | = | 6 - z | |||||||
| - | 3y | + | z | = | 7 | ||||
| z | = | 3 - y | |||||||
把 "3 - y" 代入另一个方程的 "z" 里:
| x | = | 6 - z | |||||||
| - | 3y | + | 3 - y | = | 7 | ||||
| z | = | 3 - y | |||||||
用一般的代数解法来解:
-3y + (3-y) = 7 简化成 -4y = 4,就是 y = -1
| x | = | 6 - z | |||||||
| y | = | -1 | |||||||
| z | = | 3 - y | |||||||
差不多了!
知道 y = -1,我们可以算出 z = 3-y = 4:
| x | = | 6 - z | |||||||
| y | = | -1 | |||||||
| z | = | 4 | |||||||
知道 z = 4 ,我们算出 x = 6-z = 2::
| x | = | 2 | |||||||
| y | = | -1 | |||||||
| z | = | 4 |
答案是:
x = 2、y = -1 和 z = 4
检验:留给你做!
这个方法也可以用来解 4个或更多的方程和变量……你只需重复以上步骤,直至得到答案为止。
结论:代入法好用,但需要很多时间。
消元法
消元法可以快很多……但一定要整齐地做。
"消" 的意思是移除:消元法就是把变量逐个移除,直至只剩下一个。
首先你需要要知道,我们可以安全地做以下的运算:
- 把方程乘以常数(除了零以外),
- 把两个方程相加(或相减)
如下:
为什么可以把方程相加?
看看以下两个简单的方程:
x − 5 = 3
5 = 5
我们可以把 "5 = 5" 加上 "x − 5 = 3":
x − 5 + 5 = 3 + 5
x = 8
你自己来试试,以 5 = 3+2 为第二个方程
这是允许的,因为方程两边是相等的(中间有个 = 号!)
我们也可以把方程调换位置(例如,第一个变成第二个)。
好,我们来看一个完整的例子。沿用上面的 2 个方程,2 个变量 的例子:
例子:
- 3x + 2y = 19
- x + y = 8
非常重要:一定要整齐:
| 3x | + | 2y | = | 19 | |||
| x | + | y | = | 8 |
我们的目标是从一个方程里 消除(移除) 一个变量(一个"元")。
有一个 "2y" 和一个 "y"。好,从这里下手。
把第二个方程乘以 2:
| 3x | + | 2y | = | 19 | |||
| 2x | + | 2y | = | 16 |
用第一个方程减去第二个方程:
| x | = | 3 | |||||
| 2x | + | 2y | = | 16 |
知道 x 了!
第二个方程有 "2x",把它除以 2,再减 "x":
把第二个方程乘以 ½(除以 2):
| x | = | 3 | |||||
| x | + | y | = | 8 |
把第二个方程减掉第一个方程去:
| x | = | 3 | |||||
| y | = | 5 |
大功告成!
答案是:
x = 3 和 y = 5
图是这样的:
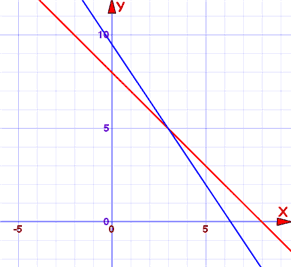
蓝线是 3x + 2y = 19 为真的地方
红线是 x + y = 8 为真的地方
在 x=3,y=5 (两条线的交叉点),两个方程都为真。那就是答案。
再举个例:
例子:
- 2x - y = 4
- 6x - 3y = 3
整齐地排好:
| 2x | - | y | = | 4 | |||
| 6x | - | 3y | = | 3 |
把第一个方程乘以 3:
| 6x | - | 3y | = | 12 | |||
| 6x | - | 3y | = | 3 |
第一个方程减去第二个方程:
| 0 | - | 0 | = | 9 | |||
| 6x | - | 3y | = | 3 |
0 - 0 = 9 ???
干啥?
很简单,无解.
| 两个方程的图是平行线: |
最后:
例子:
- 2x - y = 4
- 6x - 3y = 12
整齐地:
| 2x | - | y | = | 4 | |||
| 6x | - | 3y | = | 12 |
把第一个方程乘以 3:
| 6x | - | 3y | = | 12 | |||
| 6x | - | 3y | = | 12 |
第一个方程减去第二个方程:
| 0 | - | 0 | = | 0 | |||
| 6x | - | 3y | = | 3 |
0 - 0 = 0
没错,零等于零!
……这是因为它们其实是同一个方程…….
……所以有无穷多的解
| 是同一条线: |
以上我们看到三个可能情况的例子:
- 无(零)解
- 一个解
- 无穷多个解
消元法:3 个方程,3 个变量
我们先来看看一个比较好的方法来做消元法。
用这个方法比较不容易出错。
首先,顺序消除变量:
- 先消除 x(从第二个和第三个方程,顺序)
- 然后从第三个方程中消除 y
以下是消除的过程:
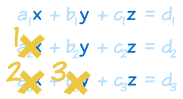
看上去像个 "三角形":
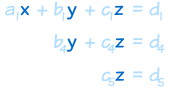
现在,从底部开始向上做(叫 "回代或倒转代换")
9代入 z 来求 y,然后代入 z 和 y 来求 x):
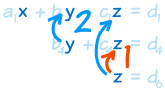
解了:

最后,有些计算可以用心算或其他的快速方法来做:
例子:
- x + y + z = 6
- 2y + 5z = -4
- 2x + 5y - z = 27
整齐地排好:
| x | + | y | + | z | = | 6 | |||
| 2y | + | 5z | = | -4 | |||||
| 2x | + | 5y | - | z | = | 27 |
首先从第二个和第三个方程中消除 x。
第二个方程没有 x……跳去第三个:
把第一个方程的两倍从第三个方程中减去(心算或在草稿纸上做就可以了):
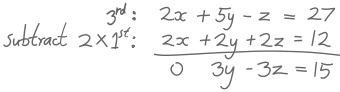
结果是:
| x | + | y | + | z | = | 6 | |||
| 2y | + | 5z | = | -4 | |||||
| 3y | - | 3z | = | 15 |
接下来,从第三个方程消除 y。
我们可以 把 (1½ 乘以第二个方程)从第三个方程减去(因为 1½ 乘 2 是 3)……
。。。。但我们可以不用分数,如果我们:
- 把第三个方程乘以 2,
- 把第二个方程乘以 3
然后这样减:
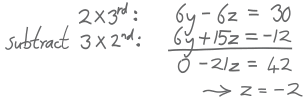
我们得到:
| x | + | y | + | z | = | 6 | |||
| 2y | + | 5z | = | -4 | |||||
| z | = | -2 |
看上去像个 "三角形"!
现在来做 "回代":
我们已经知道 z,所以 2y+5z=-4 变成 2y-10=-4,2y=6,y=3:
| x | + | y | + | z | = | 6 | |||
| y | = | 3 | |||||||
| z | = | -2 |
x+y+z=6 变成 x+3-2=6,所以 x=6-3+2=5
| x | = | 5 | |||||||
| y | = | 3 | |||||||
| z | = | -2 |
答案是:
x = 5、y = 3 和 z = -2
检验;自己来!
忠告
当你熟悉消元法后,你会觉得它比代入法容易,因为你只需要一步一步做,便可以得到答案。
但有时用代入法可以快速得到答案。
- 若只有几个方程,代入法往往会比较容易(例如,2 个方程,有时 3 个方程)
- 若有很多方程,消元法就比较容易
当然,先留心看一遍方程,看看有没有捷径。。。。。这就要依赖你的经验了……熟能生巧!