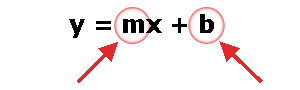线性方程
线性方程是直线的方程
以下的都是线性方程:
| y = 2x + 1 | 5x = 6 + 3y | y/2 = 3 − x |
让我们来仔细分析一个例子:
例子:y = 2x + 1是线性方程:
y = 2x+1 的图是一条直线
- 当 x 增加时,y 以 双倍的速度增加,所以我们需要 2x
- 当 x 是 0,y 已经是 1,所以也需要 +1
- 所以:y = 2x + 1
一些点的例子:
| x | y = 2x + 1 |
|---|---|
| -1 | y = 2 × (-1) + 1 = -1 |
| 0 | y = 2 × 0 + 1 = 1 |
| 1 | y = 2 × 1 + 1 = 3 |
| 2 | y = 2 × 2 + 1 = 5 |
现在自己去试试以上的点是否真的在这条线上!
不同形式
有很多不同的方式去写线性方程,它们通常有常数(像 "2" 或 "c"),并且一定要有简单变量(像 "x" 或 "y")。
例子:这些都是线性方程:
| y = 3x − 6 | ||
| y − 2 = 3(x + 1) | ||
| y + 2x − 2 = 0 | ||
| 5x = 6 | ||
| y/2 = 3 |
但线性方程的变量(像 "x" 或 "y")不能有:
例子:这些都不是线性方程:
| y2 − 2 = 0 | ||
| 3√x − y = 6 | ||
| x3/2 = 16 |
斜截式
最常见的是直线的斜截式方程:
 |
|
|||||
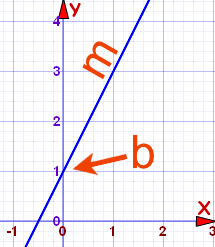
例子:y = 2x + 1
(页顶的例子,为斜截式)
- 坡度:m = 2
- 截距: b = 1
 |
来玩玩!在探索直线图中你可以看到不同 m 和 b 的效果 |
点斜式
另一个常见的形式是直线的点斜式方程:
y − y1 = m(x − x1) |
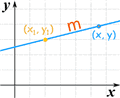 |
例子: y − 3 = (¼)(x − 2)
- x1 = 2
- y1 = 3
- m = ¼
一般式
还有直线的一般式方程:
Ax + By + C = 0 |
| (A 和 B 不能两者都等于 0) |
例子:3x + 2y − 4 = 0
- A = 3
- B = 2
- C = −4
还有其他不太常见的形式。
函数式
有时候线性方程会被写成一个函数,用 f(x)而不用 y:
| y = 2x − 3 | f(x) = 2x − 3 |
| 这些是一样的! | |
函数也不一定用 f(x) 来写:
| y = 2x − 3 | w(u) = 2u − 3 | h(z) = 2z − 3 |
| 这些也是一样的! | ||
恒等函数
有一个独特的函数,叫 "恒等函数":
f(x) = x
这是它的图:
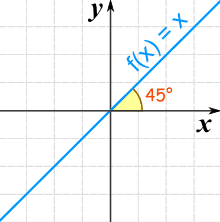
线成 45° (斜率是 1)
叫"恒等",因为函数的值(输入)是恆等于变量的值(输出):
| 输入 | 输出 |
|---|---|
| 0 | 0 |
| 5 | 5 |
| −2 | −2 |
| 。。。。。。等等 | 。。。。。。等等 |
常数函数
另一个独特的线性函数是常数函数(也称常值函数)。。。。。。它的图是一条水平直线:
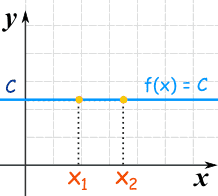
f(x) = C
无论 "x"是多少,f(x) 一定是一个常(不变的)值。
线性方程应用
你也许会喜欢去看看可以用直线来做什么: