零乘积性质
"零乘积性质" 说明:
若 a × b = 0 则 a = 0 或 b = 0 或 a=0 和 b=0
我们可以用它来解方程:
例子:解 (x−5)(x−3) = 0
"零乘积性质" 说:
若 (x−5)(x−3) = 0 则 (x−5) = 0 或 (x−3) = 0
我们只需逐一解这两个方程:
从 (x−5) = 0 我们得到 x = 5
从 (x−3) = 0 我们得到 x = 3
答案是:
x = 5 或 x = 3
以下是方程的图:
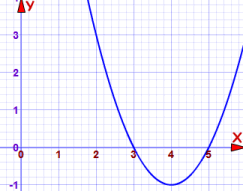
y=0,若 x=3 或 x=5
方程的标准形式
有时我们可以把方程写成标准形式,然后用零乘积性质来解:
一个方程的 "标准形式" 是:
(某个表达式) = 0
就是说, "= 0" 在右边,其他的都在左边。
例子:把 x2 = 7 写成标准形式
答案:
x2 − 7 = 0
标准形式与零乘积性质
我们来试试看:
例子:解 5(x+3) = 5x(x+3)
乍看之下,我们可以除以 (x+3),但若 x = −3,这便是 除以零。
所以我们用 "标准形式":
5(x+3) − 5x(x+3) = 0
简化成:
(5−5x)(x+3) = 0
5(1−x)(x+3) = 0
"零乘积性质" 说:
(1−x) = 0 或 (x+3) = 0
答案是:
x = 1 或 x = −3
再举个例:
例子:解 x3 = 25x
好像可以除以 x,但若 x = 0,这便是 除以零。
所以我们用标准形式和零乘积性质。
把所有项都移到左边:
x3 − 25x = 0
把 x 分解出来:
x(x2 − 25) = 0
x2 − 25 是个 平方差,可以分解为 (x − 5)(x + 5):
x(x − 5)(x + 5) = 0
我们可以看到三个答案:
x = 0、 x = 5 或 x = −5