卡方检验

卡方组

组与次数

你研究了两组人，你把他们分成三个类别，单身、已婚和离婚：

 

三个类别的数据是不同的，但是 ……

 

卡方检验  可以给你一个 "p" 值去判定！

例子："你喜欢哪种度假方式？"

  沙滩 邮轮
男 209 280
女 225 248

性别对度假方式的偏爱有影响吗？

如果性别（男或女）真的对度假方式的偏爱有影响，它们便是相依的。

我们可以用一个特别的算法（在下面有说明）算出一个 "p" 值：

p值是 0.132

通常 p < 0.05 代表变量是相依的。在这例子里，p 大于 0.05，所以我们相信变量是独立（没关联）的。

就是说，男人和女人对沙滩度假和邮轮度假的偏爱可能是没有分别的。

了解 "p"值

"p" 是变量是独立的 概率。

想象上面例子的两个随机样本里全是男人：

卡方组 1 卡方组 2
男：
沙滩 209，邮轮 280		 男：
沙滩 225，邮轮 248

在这个情形下，调查的全是男人，你会不会很可能得到这样的结果？

0.132 的 "p" 值告诉我们其实这是常常会发生的。

调查始终是随机的，每次的结果都会有点不同。

所以通常 p值要小于 0.05，我们才会说每组的结果是不同的。

我们再来看一个例子：

例子："你喜欢那种宠物？"

  猫 狗
男 207 282
女 231 242

算法（在下面解释）的结果是：

P值是 0.043

在这例子里，p < 0.05，所以这个调查结果是 "显著" 的，意思是变量不是独立的。

换句话说，因为 0.043 < 0.05，我们觉得性别与宠物偏爱是有关联的（男人和女人对猫和狗的偏爱是不同的）。

注意以上两个例子的数据是相似的，但 p值相差很大：0.132 和 0.043，所以卡方检验是一个敏感的测试！

为什么 p<0.05？

只不过是个选择！用 p<0.05 是个惯例，但我们可以用 p<0.01 来更加确定每组的调查结果是不同的，我们也可以选其他我们觉得合适的值。

计算 P值

我们怎样计算 p值？用卡方检验！

卡方检验

卡方检验的 “卡” 在英语是 "Chi"，是希腊语字母 Χ，所以“卡方”可以写成 Χ2

我们需要先记住几个重点：

第一步是声明我们的假设：

假设：一个可能是真的陈述，并且可以验证测试的。

在我们的例子里有两个假设：

把数据填在表里：

  猫 狗
男 207 282
女 231 242

把行和列分别加起来：

  猫 狗  
男 207 282 489
女 231 242 473
  438 524 962

求每项的 "期望值"：

把行的和乘以列的和，再除以全部数据的总和：

  猫 狗  
男 489×438/962 489×524/962 489
女 473×438/962 473×524/962 473
  438 524 962

结果是：

  猫 狗  
男 222.64 266.36 489
女 215.36 257.64 473
  438 524 962

从实际值减去期望值，取平方，然后除以期望值：

  猫 狗  
男 (207-222.64)2 222.64 (282-266.36)2 266.36 489
女 (231-215.36)2 215.36 (242-257.64)2 257.64 473
  438 524 962

结果是：

  猫 狗  
男 1.099 0.918 489
女 1.136 0.949 473
  438 524 962

现在把这些值相加：

1.099 + 0.918 + 1.136 + 0.949 = 4.102

卡方是 4.102

由卡方到 p

用卡方的值来求 p值是个复杂的算法，但你可以去查表或用 卡方计算器。

但先需要求 "自由度" (DF)

求自由度

(行数 − 1) 乘以 (列数 − 1)

例子： DF = (2 − 1)(2 − 1) = 1×1 = 1

结果

结果是：

p = 0.04283

大功告成！

卡方公式

这是卡方的公式：

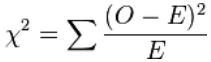
卡方公式 卡方 = (O-E)^2 / E 的总和

 

 
卡方计算器 数据索引