置信区间
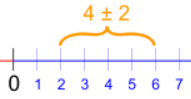
4 加减 2 的区间
置信区间是一个我们相当肯定是包含真实值的数值范围。

例子:平均身高
我们测量了 40个随机选择的男人的身高,结果是:
95%置信区间 (下面会解释计算方法)是:
175cm ± 6.2cm
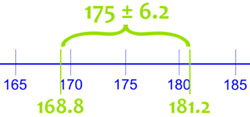
意思是所有男人(假设我们可以全部测量)的真平均身高很可能是在 168.8cm 和 181.2cm 之间。
但这可能是不对的!
"95%" 说在 95% 的实验里区间会包含真平均身高,但 5% 的实验不会。
所以我们的置信区间有二十分之一(5%)的机会不包含真平均身高。
计算置信区间
一、写下样本的数量 n,接着求这些样本的平均值 X 和 标准差 s:
- 样本的数量:n = 40
- 平均:X = 175
- 标准差:s = 20
二、决定我们用哪个置信区间,通常是 90%、95% 和 99%。然后在这查这个 "Z"值:
| Z | |
| 80% | 1.282 |
| 85% | 1.440 |
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
| 99.5% | 2.807 |
| 99.9% | 3.291 |
95% 的 Z值是 1.960
三、把 Z值代入以下的公式来求置信区间
| X ± Z | s |
| √(n) |
其中:
- X 是平均
- Z 是在上面查到的 Z值
- s 是标准差
- n 是样本的数量
结果是:
| 175 ± 1.960 × | 20 |
| √40 |
这是:
175cm ± 6.20cm
就是:从 168.8cm 到 181.2cm
± 符号后面的值叫误差界限
在以上的例子里,误差界限是 6.20cm
计算器
我们有个 置信区间计算器 来帮你计算置信区间。
再来一个例子

例子:苹果园
苹果够不够大?
果园的树上有很多苹果,你只随意选了 30个来得到以下的结果:
- 平均:86
- 标准差:5
计算:
| X ± Z | s |
| √(n) |
已知:
- X 是平均 = 86
- Z 是 Z值 = 1.960 (上面的表里的 95% 值)
- s 是标准差 = 5
- n 是样本的数量 = 30
| 86 ± 1.960 | 5 | = 86 ± 1.79 |
| √30 |
所以所有苹果的真平均值很可能是在 84.21 和 87.79 之间
真平均值
现在假设我们把所有的苹果都摘下来,然后用机器来测量它们(我们不只是纸上谈兵的!)
结果:真平均值 是 84.9
我们把全部的苹果从小到大放在地上:
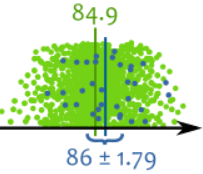
每个绿点是个苹果,
蓝点是我们的样本
我们的结果不是绝对精确的……是个随机测试……但是,真平均值是在我们算出来的置信区间 86 ± 1.79 (从 84.21 到 87.79)里
实际上,真平均值也可能不在置信区间里,但在 95% 的情况下真平均值是在置信区间里的!
真平均值会在 95% 的 "95%置信区间" 里。
我们可能会选到一个平均为 83.5 和标准差为 3.5 的样本:
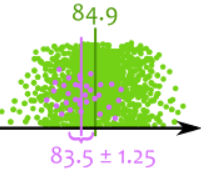
绿点是苹果,
紫点是样本
真平均值不在置信区间里。5% 的置信区间会是这样的。
那么,我们怎样才能知道样本是属于 "幸运"的 95%, 还是不幸运的 5%?除非我们真的测量所有的苹果,否则我们不会知道。
这是取样本来检验的风险,我们可能选了坏样本。
做研究的例子
这是个在长者额外锻炼的研究里应用置信区间的例子:

例子:"男" 的行里的资料是说有:
- 1,226个男人(47.6% 的人)
- 有 平均为 0.92 的 "HR"(Hazard Reduction*,意思是风险度减少)
- 和 0.88 到 0.97 的 95%置信区间(0.92±0.05)
换句话说,对所有男人来说,真正的益处有 95% 的机会是在 0.88 和 0.97 之间
* 注意:在研究里用 "HR",意思是 "Hazard Ratio"(风险比率)。这比率越低越好,所以 HR 值为 0.92 的意思是研究对象的状况变好了,1.03 代表有一点变坏了。
标准正态分布
这是基于 标准正态分布 的概念,Z值是 "z分数"
例如,95% 的 Z 是 1.960,我们可以在这里看到 95% 的值都在 -1.96 到 +1.96 之间:
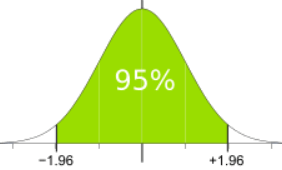
从 -1.96 到 +1.96个标准差是 95%
应用在我们的样本上就像这样:
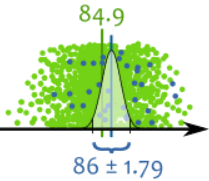
这也是从 -1.96 到 +1.96个标准差,所以包括 95%
结论
置信区间公式是
| X ± Z | s |
| √(n) |
其中:
- X 是平均
- Z 是下面的表里的 Z值
- s 是标准差
- n 是样本的数量
| Z | |
| 80% | 1.282 |
| 85% | 1.440 |
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
| 99.5% | 2.807 |
| 99.9% | 3.291 |
