连续随机变量
随机变量是随机实验结果的可能数值的集合。
例子:抛硬币:结果可以是正面或反面。
我们可以用数值来代表:正面=0 和 反面=1,这就是随机变量 "X":
简而言之:
X = {0, 1}
注意:我们也可以用 正面=100 和 反面=150 或其他数值!这完全是我们的随意选择。
连续
随机变量可以是 离散或连续的:
- 离散数据只能取某些数值(例如 1、2、3、4、5)
- 连续数据可以取一个范围(值域)里的任何数值(例如人的身高)
在随机变量入门网页(请先去看看!),我们举了很多离散随机变量的例子。
在这里,我们会介绍一个比较高级的课题:连续随机变量。
均匀分布
(也称为矩形分布)。
在均匀分布中,a 和 b 之间所有的随机变量的概率是相等的。
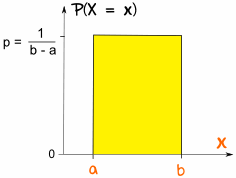
在 a 和 b 之间的任何值的概率是 p
我们也知道 p = 1/(b-a),因为所有概率的和一定是 1,所以
我们这样写:
若 a ≤
x ≤ b,P(X = x) = 1/(b−a)
否则 P(X = x) = 0

例子:老忠实间歇泉每 91分钟喷发一次。你随机来到哪里,逗留了 20分钟。你看到它喷发的概率是多少?
这其实很容易,91分之21是:
p = 20/91 = 0.22 (到2小数位)
但我们也可以用均匀分布来计算(作为练习)。
在a 和 a+20 之间的概率,求蓝色的面积:
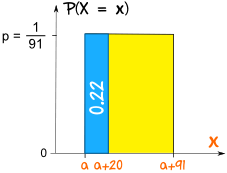
面积 = (1/91) x (a+20 - a)
= (1/91) x 20
= 20/91
= 0.22(到 2个小数位)
所以有 0.22 的可能性你会看到老忠实喷发。
如果你等 91分钟内你便一定会(p=1)看到它喷发。
但你是随机到达哪里的,所以你可能马上看到喷发,或者在 91分钟里的任何时间看到。
累积均匀分布
我们也可以有累积均匀分布:
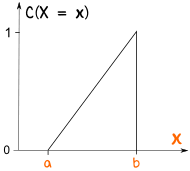
概率从 0开始,逐渐增加到 1
这种分布叫 "累积分布函数",英语是 "cumulative distribution function",简称 "CDF"
例子(续):
我们现在用以上均匀分布的 "CDF" 来计算概率:
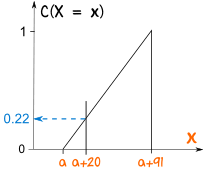
在 a+20,概率累积到大约 0.22
其他分布
| 熟悉均匀分布的应用对使用较为复杂的分布很有帮助: | 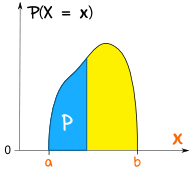 |
以下分布的通用名称是概率密度函数,英语是 "probability density function",简称 "pdf"
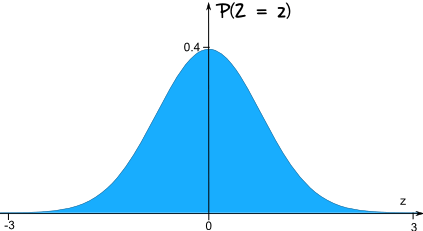
正态分布
做重要的连续分布是 标准正态分布
它非常重要,连随机变量也有独特的名字: Z.
Z 的图是个对称的钟形曲线:
通常我们需要求 Z 在两个数值之间的概率。
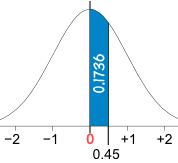
例子: P(0 < Z < 0.45)
(Z 在 0 与 0.45 之间的概率是多少) 我们用 标准正态分布表 来求答案 在 0.4的行开始,向右去到 0.45,答案是 0.1736 P(0 < Z < 0.45) = 0.1736 |
 |
总结
- 随机变量的可能值是随机实验的数值结果。
- 随机变量可以是离散或连续的。
- 一个重要的连续随机变量是标准正态变量,Z。