柏拉图固体――为什么有五个?
最简单的原因:顶点的角
为什么只有五个柏拉图固体?最简单的原因是,在一个多面体里:
 |
至少有三面(或更多)在每个顶点连接。 |
 |
在顶点的内角的和一定是小于 360度(如果等于 360°,顶点就变成平面了)。 |
我们也知道柏拉图固体所有的的面是相同的正多边形:
正三角形的内角是 60°,所以顶点可以有:
|
|
正方形的内角是 90°,所以只可以有:
|
|
正五边形的内角是 108°,所以只有:
|
|
正六边形的内角是 120°,而 3×120°=360°。 这个不行,因为如果顶点上的角加起来是 360°,就会形成一个平面,不再是顶点了。 所以不能继续下去了。 |
因此,结果是:
| 在每个顶点有: | 在顶点的角 (小于 360°) |
固体 | |
|---|---|---|---|
| 3个三角形 | 180° | 四面体 | |
| 4个三角形 | 240° | 八面体 | 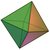 |
| 5个三角形 | 300° | 二十面体 | |
| 3个正方形 | 270° | 立方体 | 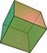 |
| 3个五边形 | 324° | 十二面体 |
任何其他的组合在顶点都会有等于或大于 360°的角,这是不可能的。例子:4个正五边形(4×108° = 432°),3个正六边形(3×120° = 360°),等等都不可能)。
这是最简单的理由。
另一个理由(拓扑学)
简而言之:不可能有多于 5个柏拉图固体,因为任何其他组合都违背关于变、顶点与面的几何定理。
欧拉公式
听过欧拉定理吗?
欧拉定理说:在任何凸多面体(包括柏拉图固体在内)中,面个数加顶点个数(角)减棱个数永远等于 2
![]() 这可以写成方程:F + V - E = 2
这可以写成方程:F + V - E = 2
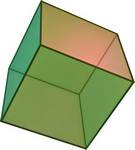 |
用立方体来试试: 立方体有 6个面、8个顶点、12条棱, 所以: 6 + 8 - 12 = 2 |
|
要深入了解欧拉公式,想象在立方体上加一条棱(例如在一个面上的对角线)。 7 + 8 - 13 = 2 |
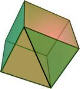 |
|
同样,如果加一个顶点(例如在一条棱的中点), 6 + 9 - 13 = 2。 "无论如何,答案还是 2" |
 |
面相接
想象一个柏拉图固体:它的面是什么形状?在每个顶点有有几个面相接在一起?
| 面可以是三角形(三条边)、正方形(四条边)等等。 | |
| 以 "s" 为每个面的边的个数。 | |
| 在每个顶点有几个面?在立方体上,有 3个面在每个顶点相接。在八面体上,每个顶点有 4个。 | |
| 以 "m" 为在每个顶点相接的面的个数。 | |
(这两个数值决定了多面体是什么图形)
把多面体展开!
现在我们把多面体的每一面剪出来。
剪出来以后,每个面是一个平面图形,边的个数是棱的双倍(因为我们把多面体的每条边一分为二)。
例子:立方体剪开后是六个正方形。
每个正方形有 4条边,总共有 24条边(立方体有 12条棱).
所以展开后边个数是立方体的棱个数 "E"的一倍 = 2E
但这也是所有剪出来的图形的边的的总数,就是 s(每面的边个数) 乘以 F(面个数)。
![]() 这可以写成方程:sF = 2E
这可以写成方程:sF = 2E
|
同样,把多面体展开时,一个顶点被剪开成几个平面的角。 以立方体为例,一个顶点被剪开成三个角,所以展开后角的个数是立方体顶点个数的三倍。 |
- 展开后,剪出来的平面的角的总数是:在原来的多面体上每一个顶点相接的面的个数(m)乘以多面体的顶点个数(V)= mV
- 展开后平面的边的总数是:原来的多面体的棱个数的两倍 = 2E
![]() 这可以写成方程:mV = 2E
这可以写成方程:mV = 2E
把方程集合在一起
我们有所有需要的方程了,把它们写在一起,并重排:
sF = 2E,所以 F = 2E/s
mV = 2E,所以 V = 2E/m
代入 "F+V-E=2":
F + V - E = 2
2E/s + 2E/m - E = 2
再做一些重排……全部除以 "2E":
1/s + 1/m - 1/2 = 1/E
"E" 是棱的个数,不能小于零,所以 "1/E" 也不能小于零:
1/s + 1/m - 1/2 > 0
就是说:
![]() 1/s + 1/m > 1/2
1/s + 1/m > 1/2
我们现在只需要用不同的:
- "s" (每面的边个数,不能小于3),
- "m" (在每个顶点相接的面的个数,不能小于 3)
来试试!
有什么可能
可能的答案是:
| s | m | 1/s+1/m | > 0.5? |
|---|---|---|---|
| 3 | 3 | 0.666…… | |
| 3 | 4 | 0.583…… | |
| 4 | 3 | 0.583…… | |
| 4 | 4 | 0.5 | |
| 5 | 3 | 0.533…… | |
| 3 | 5 | 0.533…… | |
| 5 | 4 | 0.45 | |
| 4 | 5 | 0.45 | |
| 5 | 5 | 0.4 | |
| 等等…… | …… | …… |
例子:s=5,m=5
1/s + 1/m - 1/2 = 1/E 就是
E(棱的个数) = -10,不可能!
真的有这些多面体吗?
最后,我们要确定真的有这些多面体:
| s | m | 意思 | 固体 | |
|---|---|---|---|---|
| 3 | 3 | 每个顶点有三个三角形 | 四面体 | |
| 3 | 4 | 每个顶点有四个三角形 | 八面体 |  |
| 4 | 3 | 每个顶点有三个正方形 | 立方体 |  |
| 5 | 3 | 每个顶点有三个五边形 | 十二面体 | |
| 3 | 5 | 每个顶点有五个三角形 | 二十面体 |
所以 5个都是真实的多面体。
大功告成。
Schläfli !(施莱夫利符号)
把 "s" 和 "m" 的值写在大括号 {} 之间便是多面体的施莱夫利符号(德语 "Schläfli " 符号):
例子:
- 八面体的施莱夫利符号是 {3,4},
- 二十面体的施莱夫利符号是 {3,5},
你可不可以写出其他柏拉图固体的施莱夫利符号?