几何平均数
几何平均数是一个特别的平均数,它是几个数的乘积的平方根(两个数)、立方根(三个数)等等。
例子:2 和 18 的几何平均数是多少?
- 先把数乘起来:2 × 18 = 36
- 然后(因为有两个数)开平方根:√36 = 6
写成一行:
2 和 18 的几何平均数 = √(2 × 18) = 6
就像面积相等一样!
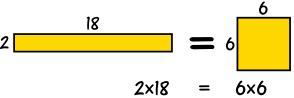
例子:10、51.2 和 8 的几何平均数是多少?
- 先把数相乘:10 × 51.2 × 8 = 4096
- 然后(因为有三个数)开立方根:3√4096 = 16
写成一行:
就好像体积相等一样:
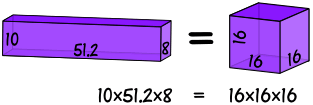
例子:1、3、9、27 和 81 的几何平均数是多少?
- 先把数相乘:1 × 3 × 9 × 27 × 81 = 59049
- 然后(因为有 5个数),开 5次方根:5√59049 = 9
写成一行:
几何平均数 = 5√(1 × 3 × 9 × 27 × 81) = 9
我不能画图来表示这个,但我可以说:
1 × 3 × 9 × 27 × 81 = 9 × 9 × 9 × 9 × 9
定义
n个数:把所有数相乘,然后开 n 次方根(写成n√)
比较正式的定义是:n个数,a1 到 an,的几何平均数是:
n√(a1 × a2 × …… × an)
应用
几何平均数可以用来比较性质非常不同的事物。

例子:你想买照相机。
- 一个相机的变焦是 200,而品质评价是 8,
- 另一个的变焦是 250, 而品质评价是 6。.
用一般的算术平均数来比较,结果是 (200+8)/2 = 104 和 (250+6)/2 = 128。变焦的数值很大,相对下,品质评价就不重要了。
但几何平均数是:
- √(200 × 8) = 40
- √(250 × 6) = 38.7……
所以,虽然变焦比品评大 50倍,品评在几何平均数里也是重要的。
这个很有用,因为如果其中一个数据改变了 25%(例如),几何平均数就大约改变了 12%。