质因子分解
质数 (素数)
质数 (素数)只能被 1 或自己整除。
同时它必须是大于一的整数。
头几个质数是: 2、3、5、7、11、13和17。。。。。。, 若你需要更多质数,我们也有个质数列表。
因子(因数)
"因子"(或"因数") 是一些数,它们乘起来的积是等于另一个数:
质因子分解
"质因子分解" 是找出 哪些质数 乘起来的积是等于原来的数。
一些例子:
例子 1: 12 的质因子是什么?
最好是从最小的质数开始。最小的质数是 2。我们看看:
12 ÷ 2 = 6
对,12 可以被 2 整除。 第一步完成了!
但 6 不是质数,所以还没做完。再试试 2 :
6 ÷ 2 = 3
对,那样可以。3 是 质数,所以有答案了:
12 = 2 × 2 × 3
你可以看到,每个因子 都是质数,所以答案是对的。
注意: 12 = 2 × 2 × 3 也可以用 幂 来显示为 12 = 22 × 3
例子 2: 147 的质因子是什么?
147 除以 2 的结果是整数而没有余数吗?
147 ÷ 2 = 73½
不是。73½ 不是整数。
试下一个质数,3:
147 ÷ 3 = 49
行了。接下来我们分解 49 为因子,结果是 7 为最小的可以整除 49 的质数 :
49 ÷ 7 = 7
我们不用再做下去了,因为所有的因子都是质数。
147 = 3 × 7 × 7
(或用幂显示为 147 = 3 × 72)
例子 3: 17 的质因子是什么?
等一等。。。。。。17 是个质数。
所以不能做下去了。
17 = 17
另一个方法
上面我们教了怎样从最小的质数开始做因子分解。
但有时最简单的是先把数分拆成任何因子。。。。。。然后再把那些因子分解为质数。
例子:90 的质因子是什么?
把 90 分解成 9 × 10
- 9 的质因子是 3 和 3
- 10 的质因子是 2 和 5
所以 90 的质因子是 3、3、2 和 5
因子树 (因数树)
"因子树" 可以帮你: 找数的 任何 因子,然后找因子的因子,继续这样做,直至不能再分解下去。
例子:48
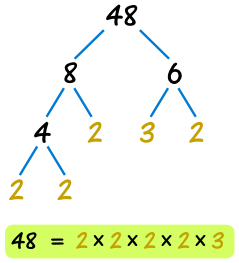
48 = 8 × 6,所以我们在 48 下面写下 "8" 和 "6"
我们继续将 8 分解为 4 × 2
然后将 4 分解为 2 × 2
最后将 6 分解为 3 × 2
不能再分解下去了,所以我们已经找到所有的质因子了。
答案是 48 = 2 × 2 × 2 × 2 × 3)
(或以幂显示为 48 = 24 × 3
为什么要找质因子?
质数只能被 1 或 自己整除,所以它不能分解为因子!
其他所有整数都可以分解为质因子。
 |
质数就像是所有数的 基本建造单位。 |
在用巨大的数工作时,这会很有用,比方在密码学里。
密码学
密码学是秘密编码的研究。对用数字来建立(或破解)密码,质因子分解是非常重要的。
这是因为对非常巨大的数来做质因子分解是非常困难的,用电脑来做也要用很长的时间。
若你想知道更多,这个学科叫 "加密" 或 "密码学"。
独一无二
还有一个重点:
每个数只有一个(独一无二!) 质因子组合。
例子: 330 的质因子是 2、3、5 或 11:
330 = 2 × 3 × 5 × 11
没有其他质数组合乘起来的积是 330。
这个念非常重要,它被称为 算术基本定理。
质因子分解工具
对了,还有一个方法。。。。。。用我们的 质因子分解工具。它可以计算大到 4,294,967,296 的质因子。
