质数和合成数
质数 (素数)只可以被 1 或 自己整除。
同时它必须是大于一的整数。
例子:7 只能被 1 或 7 整除,所以它是质数。
但 6 可以被 1、2、3 和 6整除,所以他不是质数(它是合成数)。
详细解释。。。。。。
有些整数 可以被整除,有些不可以!
例子:
6 可以被 2 或 3 整除:
6 = 2 × 3
像这样:
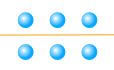 |
或 |  |
分成 2 组 |
分成 3 组 |
但 7 不能被整除:
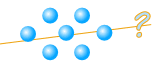
我们给它们命名:
- 一个可以被整除的数叫 合成数
- 一个不可以被整除的数叫 质数
所以,6 是合成数,但 7 是质数。
就是这样。。。。。。但还有些细节。。。。。。
不能除以分数
当我们说到质数和合成数时,我们只考虑整数!我们不会把数除以一半或四分之一。
不能除以一
我们可以 把 7 分成七个一(或一个七), 像这样:
7 = 1 x 7 |
可是任何整数都可以这样做!
因此,我们也要说不能除以 1或自己。
一个数是 质数 如果它不能被任何数整除
(除了 1 或 自己)。
例子: 7 是质数还是合成数?

- 我们不能 把 7 用 2 整除(我们会有 2 组 3 个,但剩下一个)
- 我们不能 把 7 用 3 整除(我们会有 3 组 2 个,但剩下一个)
- 我们 不能 把 7 用 4、5或6整除。
我们只能 把 7 分成一组 7 个(或七组 1个):
7 = 1 x 7 |
所以 7 只能被 1 或自己整除:
所以 7 是个 质数
同时:
一个数是合成数,如果它可以被
不是 一 或 自己 的 整数 整除。
像这样:
例子: 6 是质数还是合成数?
6 可以被 2 或 3,和 1 或 6整除:
6 = 1 × 6
6 = 2 × 3
所以 6 是个 合成数
有时一个数可以被很多种方法整除:
例子:12 可以被 1、2、3、4、6和12整除:
1 × 12 = 12
2 × 6 = 12
3 × 4 = 12
所以 12 是个 合成数
注意:
任何大于一的整数一定是 质数 或 合成数
1 怎么样?
很久以前 1 也算是质数,但现在 1 不算是质数了:
1 不是质数 也 不是合成数。
你也可以试试这个质数活动。
因子
我们也可以用因子来为质数下定义。
"因子" 是一些数,它们乘起来的积
是等于另一个数.
我们可以说:
当一个数 唯一的两个因子 是 1 和 这个数自己时,
这个数便是个 质数
这和上面定义的意思是一样的,只是用因子来表达。
记住,这只是关于 整数 (1、2、3。。。。。。等等), 无关于分数或负数。所以不要说 "我可以把 ½ 乘以 6 来得到 3"。
例子:
| 3 = 1 × 3 (唯一的因子是 1 和 3) |
质数 |
| 6 = 1 × 6 or 6 = 2 × 3 (唯一的因子是 1、2、3 和 6) |
合成数 |
从 1 到 14 的例子
突出显示除了 1 或 数字本身之外的因子:
数 |
可以被以下 整除 |
质数或 合成数? |
1 |
(1 不算质数或合成数) |
|
2 |
1, 2 |
质数 |
3 |
1, 3 |
质数 |
4 |
1, 2, 4 |
合成数 |
5 |
1, 5 |
质数 |
6 |
1, 2, 3, 6 |
合成数 |
7 |
1, 7 |
质数 |
8 |
1, 2, 4, 8 |
合成数 |
9 |
1, 3, 9 |
合成数 |
10 |
1, 2, 5, 10 |
合成数 |
11 |
1,11 |
质数 |
12 |
1, 2, 3, 4, 6, 12 |
合成数 |
13 |
1, 13 |
质数 |
14 |
1, 2, 7, 14 |
合成数 |
。。。。。。 |
。。。。。。. |
。。。。。。 |
当除了 1 或 数自己以外还有因子时,数便是 合成数。
问题: 15 是质数还是合成数?
为什么要学质数或合成数?
因为我们能把 合成数 "拆开为" 质因子。
 |
可以这样说:质数是所有数的 基本建造单位。 而合成数是由质数相乘而得到的。 |
看看实际行动:
这就是为什么它们叫"合成"数,因为合成的意思是"合起来的东西"
这理念非常重要,它被称为 算术基本定理。
数学上很多难题都可以用把合成数"拆开" 为质因子的方法去解。互联网上的保安也有很大部分是基于质数的数学的。

