NP完全――粗略指南

这只是 "NP完全" 的粗略指南，并不是精确的定义，但可以帮助你了解NP完全的概念。

这些是我个人的想法，不一定是 "严格"的。

这是关乎"求解时间"的

你可以测量电脑程序去解越来越困难的问题所需要的时间（例如排序有 10项的列、20项的列、30项的列等等），然后做一个图来估计程序时间的函数。

但如果时间按指数规律或阶乘规律增长，程序就不是 "P"问题（不可以在多项式时间内求解）。

P：可以在多项式时间内求解。（P 源自多项式的英语单词 Polynomial）
 （需要的时间可以用多项式来定义）

奇妙电脑无所不能

在 "NP" 里的 "N" 的意思是没有一般普通电脑的限制，例如逐步求解。"N" 的意思是 "非确定性"（源自英语单词 Non-deterministic）。这个（假想的）奇妙电脑可以同时进行多个运算，或准确猜测正确的运算方法等等。

这个 "N" 电脑可以在 "P" 时间内解更多问题――例如如果需要的话，它可以复制自己。

奇妙电脑不是超级电脑（超级电脑只不过是很快的普通电脑），它是个 "非确定性" 电脑。我叫它做奇妙电脑因为它的确是奇妙的！

所以一个需要用大幅增长的时间来解越来越困难的问题的程序（就是，非P问题）可以用这个奇妙的 "N" 电脑来很快求解，这些程序就是 "NP"问题。"NP" 的意思是 "如果不受正常逐步求解的电脑运算所限制，问题就可以在多项式时间里求解".

NP：可以用非确定性方法在
多项式时间内求解。
（也包括 P问题）

 

奇妙电脑也可以做普通电脑可以做的

因为 "N"电脑也可以做任何普通电脑可以做的，"P"问题也是 "NP"问题。

所以，容易的问题都是 "P"问题（也是"NP"），但真正困难的问题是"不是 P问题的 NP问题"。这些问题叫 "NP完全"问题（NPC问题）

就像说：有普通人可以做的事（"P"），有超人可以做的事（"SP"），但也有*只有*超人才能做的事（"SP完全"）。

NP完全：只可以用非确定性方法
才能在多项式时间内求解.

NP完全可能不存在

数学家相信如果一个 "NP完全"问题可以在 "P" 时间内求解，*所有* "NP完全"问题都可以用同一个方法求解。在这情形下，"NP完全"问题就不存在了。

 

旅行推销员问题

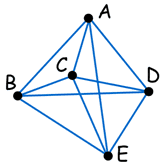
"NP完全"问题的典型例子是旅行推销员问题。

你需要到 5个城市推销货品，你知道城市之间的距离。 最短的来回（起点和终点相同）路程是什么？ABCEDA? ADECBA?

最简单的求解方法是尝试所有的可能。

但这个方法只是用来解小规模的问题才是可行的。多加一个城市就需要把这个城市和以前每个可能合起来逐个尝试。

所以这个方法需要 "阶乘时间time"：t = n!

（正确的公式是 t = (n-1)!，还是阶乘的。）

假想程序需要 1秒来解 20个城市的问题，

• 21个城市就要 21秒。
• 22个城市就要大约 462秒（超过 7分钟），
• 30个城市就要 3百万年。哎唷!

有特别的方法来把问题分拆成一系列的小问题（叫 "动态规划程序设计"），但最短的时间还是 指数时间：t = 2ⁿ （2 的 n 次方）

所以如果程序解 1个城市的问题需要 1秒，30个城市就需要 10分钟，60个城市就要 35,000年（还是有点长）。

但如果我们用上面的"奇妙电脑"，电脑就可以复制自己来同步尝试所有的可能，而大幅减少解问题的时间。

NP困难

当所有NP问题可以在多项式时间内归约到一个问题，这个问题就是个 "NP困难"问题。

NP困难：至少与 NP问题一样难，可能更难。

 

 

我希望这个 "简单组略" 的入门说明使得你略为了解这些概念 …… 如果你有兴趣的话，你应该去阅读一些更严格的文献。