对数可以是小数
在对数入门中,我们知道对数解答像以下的问题:
有多少个 2 和自己相乘可以得到 8?
答案: 2 × 2 × 2 = 8,所以需要 3 个 2 来得到 8
所以对数是 3
我们写:"需要3个2相乘来得到8" 为
log2(8) = 3
所以以下两个是相同的:
例子:log10(100) 是多少?
10 × 10 = 100
把 2 个 10 相乘的积是 100,所以:
log10(100) = 2
注意:用指数来表达,这是:102 = 100
我们现在问一个新的问题:
例子:log10(300) 是多少?
10 × 10 = 100
10 × 10 × 10 = 1000
不行!不是太小就是太大。
把 两个 10 相乘不够,但把 三个 10 相乘又太大。。。。。。
。。。。。。那 两个半呢?
半个乘。。。。。。
乘以平方根就像做半个乘。
我们来试试:
例子:log10(300) (续)
试试用 10 与自己相乘 两次半:
10 × 10 × √10
=
10 × 10 × 3.16...
= 316....
离 300 很近,所以我们可以说:
log10(300) ≈ 2.5 (大约)
换句话说,把10和自己相乘两次半的结果是大约 300。
(注意:用指数来表达是 300 ≈ 102.5)
在图上是这样:
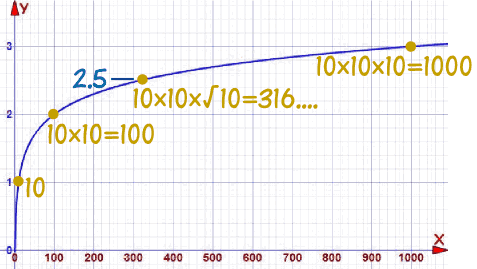
2: 10 × 10 = 100
2.5: 10 × 10 × √10 = 316....
3: 10 × 10 × 10 = 1000
故此,对数不只是像 2 或 3 的整数:2.5也可以。
我们可以找更多的值(用立方根,四次方根等等),像 2.75 或 1.9055等等。
我们不需要用方根等等来计算找对数,因为。。。。。。
。。。。。。在现实世界里,还是用计算器比较方便!
使用计算器
 |
例如,"log" 键是用来计算以 "10为底" 的对数。 |
例子:用计算器来算, log10(300)是多少?
在计算器打入 300,按 log键
答案:2.477。。。。。。
这就是说,需要把 2.477。。。。。。 个 10 相乘来得到 300:
log10(300) = 2.477。。。。。。
我们先前的估计,2.5,也不赖。
注意:用指数来表达,这是:102.477。。。。。。 = 300
例子: log10(640)是多少?
在计算器打入 640,按 log 键
答案:2.806。。。。。。
这就是说,需要把 2.806。。。。。。个 10 相乘来得到 640:
log10(640) = 2.806。。。。。。
用上面的图,看看在 x=640 的值是多少
注意:以指数来表达,这是:102.806... = 640
就是这样。。。。。。对数(用多少个数和自己相乘)真的可以是小数。