对数入门
在最简单的层面,对数解答以下问题:
多少个既定的数相乘会等于另一个数?
例子:多少个 2 相乘会等于 8?
答案:2 × 2 × 2 = 8,所以需要把 3 个 2 相乘来得到 8
所以对数是 3
怎样写
我们这样写"3个2相乘的积为8":
log2(8) = 3
所以这两个是相同的:
相乘的数叫 "底",而对数的符号是 "log",所以我们可以说:
- "8的以2为底的对数是 3"
- 或 "8的log(以2为底)是 3"
- 或 "8以2为底的log是 3"
请留意,这牵涉到三个数:
- 底:相乘的数(在以上的例子的 "2")
- 多少个底相乘(3个,这就是 对数)
- 相乘起来的积(在以上的例子的 "8")
更多例子
例子: log5(625) 是多少?
问题是 "需要多少个 5 相乘,来得到 625?"
5 × 5 × 5 × 5 = 625,所以需要4 个 5
答案:log5(625) = 4
例子:log2(64) 是多少?
问题是 "需要多少个 2 相乘,来得到 64?"
2 × 2 × 2 × 2 × 2 × 2 = 64,所以需要 6 个 2
答案:log2(64) = 6
指数
指数与对数是有关联的。我们来看看。。。。。。
指数的意思是用多少个数和自己相乘。 在这例子里:23 = 2 × 2 × 2 = 8 (3 个 2 乘在一起的积是 8) |
所以对数解答这样的问题:
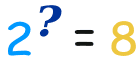
这样去解答:
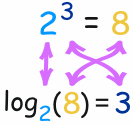
对数告诉我们指数是多少!
在这例子, "底" 是 2, "指数" 是 3:
故此,对数解答这问题:
需要什么指数
(把一个数变成另一个数)?
一般的情形是:
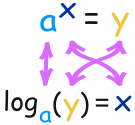
例子:log10(100) 是多少?
102 = 100
指数需要等于 2,方可把 10变成 100,所以:
log10(100) = 2
例子:log3(81) 是多少?
34 = 81
指数需要等于 4,方可把 3 变成 81,所以:
log3(81) = 4
常用对数:底为 10
有时候写对数时,底是不写的:
log(100)
通常这代表底是 10。
这叫 "常用对数"。工程师时常用常用对数。
在计算器上是 "log" 键。
意思是需要多少个 10 相乘来得到一个数。
例子:log(1000) = log10(1000) = 3
自然对数: 底为 "e"
另一个时常用的底是 e(欧拉数),大约的值是 2.71828。

这叫 "自然对数"。数学家时常用自然对数。
在计算器上是 "ln" 键。
意思是需要多少个 "e" 相乘来得到一个数。
例子:ln(7.389) = loge(7.389) ≈ 2
因为 2.718282 ≈ 7.389
可是,有时会引起混淆。。。。。。!
数学家用 "log" (而不是 "ln")来代表自然对数。这便会引起混淆:
| 例子 | 工程师演绎 | 数学家演绎 | |
|---|---|---|---|
| log(50) | log10(50) | loge(50) | 混淆 |
| ln(50) | loge(50) | loge(50) | 没混淆 |
| log10(50) | log10(50) | log10(50) | 没混淆 |
所以当你看见 "log" 时,必须找出底是多少!
对数可以是小数
以上的例子里的对数全是整数(像2或3),但对数可以是小数,像 2.5 或 6.081等等
例子:log10(26)是多少?
 |
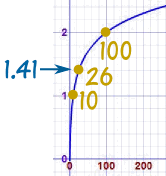
把 26 打进计算器,按 log键 答案是: 1.41497。。。。。。 |
这对数的意思是 101.41497。。。。。。 = 26
(10 的指数为 1.41497。。。。。。 等于 26)
在图上像这样: 很漂亮的图,对不? |
 |
去对数可以是小数了解更多。
负对数
| − | 负?对数是基于乘法。 那么,乘的相反是什么?除! |
负对数的意思是需要除以一个数多少次。
可以只除一次:
例子:log8(0.125)是多少?
1 ÷ 8 = 0.125,
所以 log8(0.125) = −1
也可以除很多次:
例子:log5(0.008)是多少?
1 ÷ 5 ÷ 5 ÷ 5 = 5−3,
所以 log5(0.008) = −3
这是合情合理的
乘和除是属于同一个简单的规律。
我们来看看一些以10为底的对数:
| 数 | 多少个 10 | 对数(以10为底) | ||
|---|---|---|---|---|
| 。。。等等。。。 | ||||
| 1000 | 1 × 10 × 10 × 10 | log10(1000) | = 3 | |
| 100 | 1 × 10 × 10 | log10(100) | = 2 | |
| 10 | 1 × 10 | log10(10) | = 1 | |
| 1 | 1 | log10(1) | = 0 | |
| 0.1 | 1 ÷ 10 | log10(0.1) | = −1 | |
| 0.01 | 1 ÷ 10 ÷ 10 | log10(0.01) | = −2 | |
| 0.001 | 1 ÷ 10 ÷ 10 ÷ 10 | log10(0.001) | = −3 | |
| 。。。等等。。。 | ||||
留心看这列表,注意到正、零和负对数全都是属于同一个(相当简单的)规律。
英语 "Logarithm"
对数的英语 "Logarithm" 为苏格兰数学家约翰·奈皮尔(公元1550-1617)所创,源自希腊字 logos,意思是"比例或字";而 arithmos 的意思是 "数"。。。。。。合成一个字就是 "比例数"!