用初等行运算
来求逆矩阵
也称 高斯-若尔当 方法
这是个有趣的求逆矩阵方法。。。。。。
| 。。。。。。玩玩这些行 (加、乘或对换) 直至把矩阵 A 变成单位矩阵 I。 |
在单位矩阵上也做一模一样的运算, 单位矩阵便会奇妙的变成 逆矩阵! |
"初等行运算"是简单的运算,像把行相加,乘,对换位置。。。。。。我们先来看例子:
例子:求 "A" 的逆:
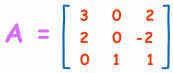
把给予的矩阵 A 与 单位矩阵 I 并排写下来:

(这叫 "增广矩阵")
单位矩阵
"单位矩阵" 在矩阵中的意思是和数字里 "1" 的意思相若的:
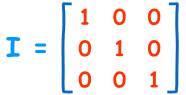
3x3 单位矩阵
- 它是 "方形"的(相同数目的行和列),
- 它有 1 在对角线上,0 在所有其他位置上,
- 它的 符号是大写字母 I。
接着我们尽力去把 "A" (在左边的矩阵)变成单位矩阵。我们的目标是把矩阵 A 的对角线变成全是 1,而在所有其他位置都是 0 (单位矩阵)。。。。。。在右边的矩阵也做同样的运算。
我们只能做这些 "初等行运算":
- 对换两行的位置
- 把一行里的每个元素乘以或除以一个常数
- 把一行加上另一行的倍,并取代前者。
以上一定要以全行运算,像这样:
先把 A 写在 I 左边
把 行2 加到 行1 上,
把 行1 乘以 5,
把第一行的两倍从第二行减去,
把第二行乘以 -1/2,
把第二和第三行对换位置,
最后,把第三行从第二行减去,
做好了!
矩阵 A 变成单位矩阵。。。。。。
。。。。。。同时单位矩阵便成 A-1了
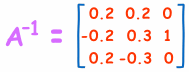
大功告成!像玩魔术一样,和解谜题一样好玩。
注意:没有 "绝对正确" 的方法来做这个,只有不停尝试,直至成功为止。“自古成功在尝试”!
(把这答案与在 用余子式、代数余子式和伴随 来求逆矩阵 里求的逆矩阵比较一下。是不是一样?你喜欢哪个方法?)
较大的矩阵
求较大的矩阵的逆矩阵都是用同样的方法。我们用这个 4x4 矩阵来试试:

开始:

试试自己来做(我一开始会把第一行除以 4,但你可随意用你自己的方法)。
为什么这能行
我是这样想:
而 "1/8" 是 8 的(乘)逆 |
用比较专业的语言来说: 故此,A 变成 I (因为 A-1A = I) |