立方差
这是多项式相乘的一个特别情况,得到的结果是:a3 - b3
多项式
多项式看起来像这样:
| 多项式例子 |
立方差
立方差是多项式相乘的一个特别情况:
(a−b)(a2+ab+b2) = a3 − b3
有时候我们在求解时会遇到它,所以把它记住是挺有用的。
在这里你可以看到它的来龙去脉。
几何例子
看看两个大小分别为 x 和 y 的立方体:
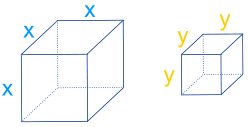
大小为 "x" 的立方体可以被分拆为四个长方体, A 长方体是大小为 "y" 的立方体:
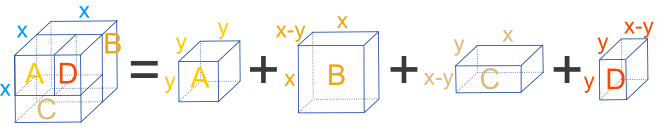
这些长方体的体积是:
- A = y3
- B = x2(x – y)
- C = xy(x – y)
- D = y2(x – y)
但放在一起,A、B、C 和 D 凑成的大立方体的体积是 x3:
| x3 | = | y3 + x2(x – y) + xy(x – y) + y2(x – y) |
| x3 – y3 | = | x2(x – y) + xy(x – y) + y2(x – y) |
| x3 – y3 | = | (x – y)(x2 + xy + y2) |
对了!公式没错!
立方和
还有"立方和"的公式
把 b 的正负号倒转,这便成为:
(a+b)(a2−ab+b2) = a3 + b3
(留意 "ab" 前面也有个负号)