代数――代换
"代" 的意思是把一样东西换为另外一样东西。
代换
在代数里,"代换(或代入)" 的意思是用数来代替字母:
| 若: |
|
||||||
| 当 x=6 …… | |||||||
| ……便可以把 6 "代入" x: |
|
例子:若 x=2,10/x + 4 是多少?
把 "2" 放到 "x" 的位置:
10/2 + 4 = 5 + 4 = 9
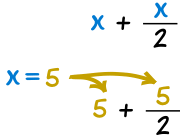
例子:若 x=5,x + x/2 是多少?
把 "5" 放到 "x" 的位置:
5 + 5/2 = 5 + 2.5 = 7.5
例子:若 x=3 及 y=4,x2 + xy 是多少?
把 "3" 放到 "x" 的位置,把 "4" 放到 "y" 的位置:
32 + 3×4 = 3×3 + 12 = 21
例子:若 x=3 (但 "y" 是未知数),x2 + xy 是什么?
把 "3" 放到 "x" 的位置:
32 + 3y = 9 + 3y
(只能做到这里了)
正如以上的例子所示,有时我们不能得到一个数,而只能得到一个比较简单的公式。
负数
代入负数时,在数的两边加上括号 ( ) 就不容易出错。
例子:若 x = −2,1 − x + x2 是多少?
把 "(−2)" 放到 "x" 的位置:
1 − (−2) + (−2)2 = 1 + 2 + 4 = 7
在这个例子:
- − (−2) 变成 +2
- (−2)2 变成 +4
因为有以下的规则:
| 规则 | 加或 减 |
乘或 除 |
||
|---|---|---|---|---|
| 相同的正负号变成 正号 | 3+(+2) = 3 + 2 = 5 | 3 × 2 = 6 | ||
| 6−(−3) = 6 + 3 = 9 | (−3) × (−2) = 6 | |||
| 不同的正负号变成 负号 | 7+(−2) = 7 − 2 = 5 | 3 × (−2) = −6 | ||
| 8−(+2) = 8 − 2 = 6 | (−3) × 2 = −6 |