求中心值
如果你有两个或更多的数,知道它们的 "中心值" 往往会很有用。
2个数
如果只有 2个数,这就很简单:取两个数的正中点就行了。
例子:3 和 7 的中心值是多少?
答案:中间的一半,就是 5。
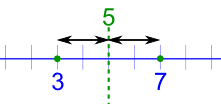
算法是把 3 和 7 相加然后除以 2:
3个数或更多
三个或更多的数也一样:
例子:3、7 和 8 的中心值是多少?
答案:把 3、7 和 8 相加然后除以 3(因为有 3个数)
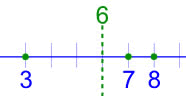
注意我们除以 3,因为有 3个数 …… 这是非常重要的!
平均
上面计算的是 平均:
平均:把数相加然后除以数的个数。
可是,有时候平均可能不管用:
例子:生日派对游戏
白叔叔想知道生日派对里小孩的平均年龄,好等他安排游戏。
派对里有 6个 13岁的小孩和 5个 1岁的婴儿。
把所有的岁数加起来,然后除以 11(因为有 11个数):
 |
平均岁数大约是 7½,所以他安排了跳跃城堡游戏! 那些十三岁的觉得游戏很幼稚, |
平均准确是准确了,但没用。
中位数
但你也可以用 中位数:把所有的数顺序排列,然后选在正中的一个:
例子:生日派对游戏(续)
把岁数顺序排列:
1、1、1、1、1、13、13、13、13、 13、13
选在正中的一个:
1、1、1、1、1、13、13、13、13、13、13
中位岁数是 13 …… 所以我们来跳舞!
有时可能会有两个数在正中。如果是这样,便取这两个数的平均值:
例子:3、4、7、9、12、15 的 中位数是多少
有两个数在正中:
3、4、7, 9、12、15
我们取它们的平均值:
中位数是 8
众数
众数 是出现最多的数:
例子:生日派对游戏(续)
把岁数分组:
1、1、1、1、1、13、13、13、13、13、13
"13" 出现了 6次,"1" 只出现了 5次,所以众数是 13。
怎样去记?想: "众"多
可是,众数有点巧妙,有时会有几个众数。
例子:3、4、4、5、6、6、7 的众数是多少
嗯 …… 4 出现了两次,但 6 也出现了两次。
所以 4 和 6 都是众数。
有两个双众数的情况叫 "双众数",有三个或以上的众数叫 "多众数"。
离群值
离群值 是数据里与其他数值分开的数值("离"开其他的"群"值。)
离群值可以导致平均值有很大的改变,所以我们可以不用它们(但要明示)来计算平均值,或者用中位数或众数。
例子:3、4、4、5 和 104
平均:相加,除以 5(有 5个数):
24 不能代表这五个数!
拿走 104 后,平均是:
好多了,但一定要明确表示你没有用离群值。
中位数:数已经是顺序排列了,所以就用正中的数, 4:
3、4、4、5、104
众数:4 出现最多,所以众数是 4
3, 4、4、5、104
结论
另外还有其他的方法去计算中心值,但最常用的是平均、中位数和众数。
用最适合当前数据的方法,最好是三个都用!