相关
当两组数据有强烈的相互关系时，我们说它们高度相关。
- 若两组的值一起增大，我们称之为正相关，
- 若一组的值增大时，另一组的值减小，我们称之为负相关
我们在这里讲的是线性相关（跟随直线的相关）。
相关可以用值来表达：
- 1 是完全正相关
- 0 是无相关（没有相互关系）
- -1 是完全负相关
这个值显示相关有多强（并不代表线有多陡）以及相关是正相关还是负相关。
例子：冰淇淋销量
冰淇淋店记录了每天的冰淇淋销量和当天的气温。这是过去 12天的数据：
| 冰淇淋销量与气温 | |
| 气温 °C | 冰淇淋销量 |
|---|---|
| 14.2° | ￥215 |
| 16.4° | ￥325 |
| 11.9° | ￥185 |
| 15.2° | ￥332 |
| 18.5° | ￥406 |
| 22.1° | ￥522 |
| 19.4° | ￥412 |
| 25.1° | ￥614 |
| 23.4° | ￥544 |
| 18.1° | ￥421 |
| 22.6° | ￥445 |
| 17.2° | ￥408 |
这是数据的散布图：
显而易见，气温越高，销量也越高。关系强，但不是绝对的。
相关值是 0.9575 …… 在下面你可以看到这是怎样算出来的。
相关对曲线不适用
相关计算只在有直线关系时才适用。
冰淇淋销量例子：热浪袭击！
实在太热了，人们都躲在家里，冰淇淋销量开始下跌了。
这是最近的图：
相关值是 0："无相关" …… ！!
相关值算出来是 0 （我算的），意思是 "无相关"。
但我们可以看到数据其实是有相互关系的：数据跟随一条曲线，最高点在大约 25° C。
可是线性相关计算不能显示出来.
这个故事的寓意是：画个散布图看看！
肉眼有时可以看到计算不能显示的。
相关不等于因果关系
"相关不等于因果关系" …… 就是说，相关不代表一个现象导致另一个（相关可能有其他的原因）。
例子：墨镜与冰淇淋
冰淇淋店用冰淇淋销量和百货公司的墨镜销量比较：
墨镜和冰淇淋有高的相关
这代表墨镜使到人们想吃冰淇淋吗？
例子：实例！
几年前一个员工调查发现 "修读工余课程" 和高病假 有很强的正关联。
这是不是代表：
- 读书使到员工生病？
- 容易生病的人喜欢读书？
- 或者员工报病假去读书？
只有再多做些研究才可以知道是为什么。
怎样计算
我是怎样计算上面 0.9575 这个答案的？
我用 "皮尔森相关系数"。有电脑软件可以计算这个系数，例如 Excel 里的 CORREL() 函数，或我们的 LibreOffice Calc ……
…… 但你可以自己这样做：
设 "x" 和 "y" 为两组数据（在我们的例子，温度是 x，冰淇淋销量是 y）：
- 一、分别求 x 和 y 的平均值
- 二、从每个 x值减去 x 的平均值（以 "a" 来代表结果），y 也做同样的计算（以 "b" 来代表结果）
- 三、求：每一个值的 a × b、a2 和 b2
- 四、把 a × b 加起来、 a2 加起来、b2 加起来
- 五、用 a × b 的总和除以 [(a2 的总和) × (b2 的总和)] 的平方根
这是第一个冰淇淋例子的计算（舍入到 1个或 0个小数位）：
写成公式是；
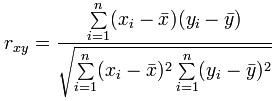
其中：
- Σ 是 总和符号
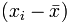是每个 x值减去 x 的平均值（在上面叫 "a"）
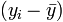是每个 y值减去 y 的平均值（在上面叫 "b"）
你通常不需要这样手动计算，但现在你至少知道计算的程序。
程序员提示
你可以一遍做好：把 x、y、x2、y2 和 xy 各自加起来（不用做上面 a 或 b 的计算），然后用这个公式：
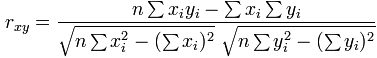
其他方法
还有其他的方法去计算相关系数，例如 "斯皮尔曼等级相关系数"，但我喜欢用像上面那样的列表来做。