散布图
散布(XY)图用点来显示两组数组的关系。 在这个例子里,每一点显示一个人的体重,相对他的身高. (数据是以 "笛卡尔 (x,y) 坐标" 画在图上) |
例子:
冰淇淋店记录了每天的冰淇淋销量与当天中午的气温。这是过去 12天的记录:
| 冰淇淋销量与气温 | |
| 气温 °C | 冰淇淋销量 |
|---|---|
| 14.2° | ¥215 |
| 16.4° | ¥325 |
| 11.9° | ¥185 |
| 15.2° | ¥332 |
| 18.5° | ¥406 |
| 22.1° | ¥522 |
| 19.4° | ¥412 |
| 25.1° | ¥614 |
| 23.4° | ¥544 |
| 18.1° | ¥421 |
| 22.6° | ¥445 |
| 17.2° | ¥408 |
这是数据的 散布图:
在图上很容易看到温暖的天气导致较大的销量,但关系不是绝对的。
最优拟合线
我们也可以在散布图上画一条"最优拟合线"(也称为 "趋势线"):
尽量把线接近最多的点,并且在线上面和线下面有一样多的点。
例子:海平面上升
这是海平面上升的散布图: |
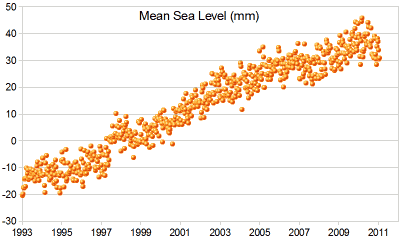 |
| 我在图上也画了一条 "最优拟合线"。 | 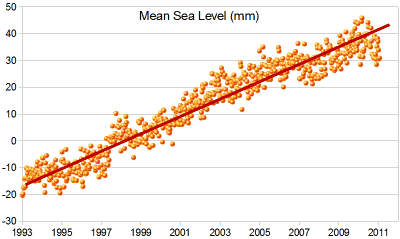 |
内插和外推
内插是在数据集合里面求一个值。
在这里我们用线性内插来估计在 21 °C 时的销量。
外推是在数据集合外面求一个值。
在这里我们用线性外推来估计在 29 °C(大于我们所有的数据)时的销量.
小心:外推可能导致误导性结果,因为我们离开了我们数据的范围。
除了用图(如上)之外,我们还可以创立一个公式。
例子:直线方程
从上面的图里的两点,我们可以估计一个 直线方程
我们来估计在线上接近实际数据的两点:(12°, ¥180) 和 (25°, ¥610)
先求坡度:
| 坡度 "m" | = y 的改变 x 的改变 |
| = ¥610 − ¥180 25° − 12° | |
| = ¥430 13° | |
| = 33 (舍入) |
把坡度和点 (12°,¥180) 代入 "点斜式" 公式:
y − y1 = m(x − x1)
y − 180 = 33(x − 12)
y = 33(x − 12) + 180
y = 33x − 396 + 180
y = 33x − 216
内插
我们可以用这个方程来内插在 21° 的销量:
y = 33×21° − 216 = ¥477
外推
也可以外推在 29° 的销量:
y = 33×29° − 216 = ¥741
结果跟在图上得到的差不多,但这不代表结果是比较(或比较不)精确的――它们全是估计值。
不要在远离原始数据范围用外推法!你以为在 0° 时的销量会是多少?
y = 33×0° − 216 = −¥216
嗯……负 ¥216?外推得太远了!
注意:上面我们用了线性(基于直线)内插和外推,但也有很多其他种类的内插和外推法,例如我们可以用多项式的曲线。
相关
当两组数据有紧密的关联时,我们说他们是高相关的。
相关的英语是 "Correlation",是从 "Co-"("一起")和 "Relation"("关系")合并而成的字。
- 正相关是两组数值一起增加,
- 负相关是当一组数值增加时,另一组数值减小
像这样:
(去学习 更多相关)
负相关
相关可以是负的,意思是有相关,不过一个数值增加时,另一个数值减小。
例子:出生率与入息比较富裕的国家的出生率通常比较低。
这是 100个国家的散布图。 |
|
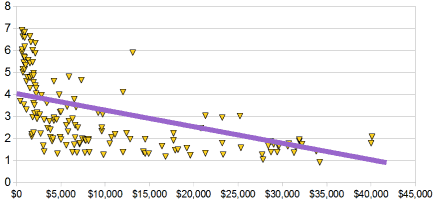
数据有负相关(线向下倾斜)
注意:我用了直线拟合线,但可能曲线会更好,你觉得呢?