不规则多边形的面积
简介
我想和你分享一个计算求一般多边形面积的巧妙方法
多边形可以是规则的(所有角和边都是相等的)或不规则的
 |
 |
| 规则 | 不规则 |
多边形例子
我们用这个多边形为例:
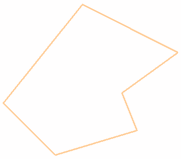
坐标
第一步是把所有顶点(角)转换成坐标,如图所示:
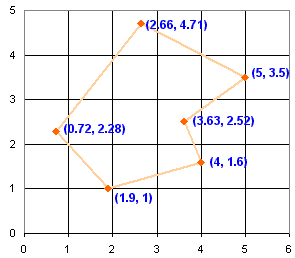
一条线段下面的面积
接下来,求每条线段下面与 x轴之间的面积。
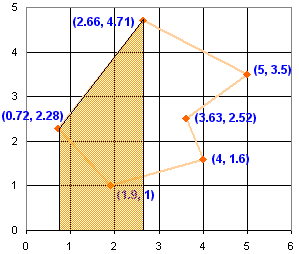
我们怎样去求每个面积?
求两个高度的平均值,再乘以宽度
例子:在上面突显的图形中,我们求两个高度("y" 坐标 2.28 和 4.71)的平均:
(2.28+4.71)/2 = 3.495
求宽度("x" 坐标 2.66 和 0.72 的差)
2.66-0.72 = 1.94
面积是 宽度×高度:
1.94 × 3.495 = 6.7803
加起来
最后把全部面积加起来!
但窍门是前进时(正宽度)的面积要加上,而后退时(负宽度)的面积便要减去。
一直顺时针方向走,并且永远用第二个"x"坐标减去,计算就不会出错,像这样:
| 从 | 到 | |||||
|---|---|---|---|---|---|---|
| x | y | x | y | 平均高度 | 宽度 (+/-) | 面积 (+/-) |
| 0.72 | 2.28 | 2.66 | 4.71 | 3.495 | 1.94 | 6.7803 |
| 2.66 | 4.71 | 5 | 3.5 | 4.105 | 2.34 | 9.6057 |
| 5 | 3.5 | 3.63 | 2.52 | 3.01 | -1.37 | -4.1237 |
| 3.63 | 2.52 | 4 | 1.6 | 2.06 | 0.37 | 0.7622 |
| 4 | 1.6 | 1.9 | 1 | 1.3 | -2.1 | -2.7300 |
| 1.9 | 1 | 0.72 | 2.28 | 1.64 | -1.18 | -1.9352 |
| Total: | 8.3593 | |||||
图是这样的:
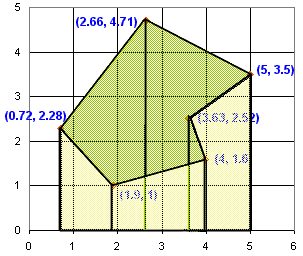
做好了!面积是 8.3593
多边形面积工具
很感谢你看到这里!作为奖励,你可以用求多边形面积绘图工具来帮你做所有的计算。这工具也接受手动输入坐标。