用扇形来求圆的面积
这是导出圆形面积公式的一个方法:
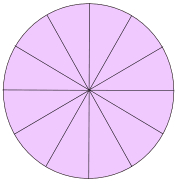
把圆切成相同的扇形(在这个例子里是 12个扇形)
把其中一个扇形再一分为二。我们现在有十三个扇形――把它们标记为 1 到 13:
把 13个扇形像这样重排:
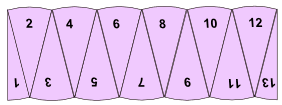
看上去像个矩形:
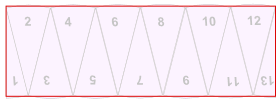
矩形的(近似)高度和宽度是多少?
高度是圆的半径:看看扇形1 和扇形13,在圆形里它们的高度是圆的 "半径"。
矩形的宽度(其实是一条"弯曲不平" 的线)是环绕圆的一半……就是圆周的一半。
我们知道:
圆周 = 2 × π × 半径
所以矩形的宽度大约是:
圆周的一半 = π × 半径
我们得到(大约):
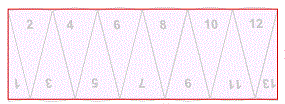 |
半径 |
| π × 半径 |
我们用把宽度乘以高度来求矩形的面积:
面积 = (π × 半径) × (半径)
= π × 半径2
注意:矩形和扇形合成的 "图形" 并不是完全一样的。
但如果我们把圆切成 25个扇形(23个 15°、2个 7.5°),结果便会更好。
切成的扇形越多,答案就越准确。
结论
圆形的面积 = π r2
