动量
动量是物体倾向同一方向继续移动的物理量。
很难使这辆货车停下来……

……它有很多动量。
更快?更多动量!
更重?更多动量!
动量是质量乘以速度。符号是小写英语字母 p:
p = m v

例子:1500千克重的汽车以 28米每秒(大约 100千米每小时或 60英里每小时),它的动量是多少?
p = m v
p = 1500千克 × 28米每秒
p = 42,000千克米每秒
动量的单位是:
- kg m/s(千克米每秒),也就是
- N s(牛顿秒)
它们是相同的!1 kg m/s = 1 N s
在这里我们两个单位都会使用。
注意:动量的方向就是速度的方向。
冲量
冲量是动量的改变。Δ 是 "改变" 的符号,所以:
冲量是 Δp
力可以被计算为 动量相对于时间的改变(称为动量的 "时间变化率"):
F = Δp Δt


例子:你的体重是 60千克,你以 3米每秒的速度冲到墙壁。
墙壁在 0.05秒内把你停下。力度是多少?
把墙加上软垫后,你在 0.2秒内停下。力度是多少?
先求冲量:
Δp = m v
Δp = 60千克 × 3米每秒
Δp = 180千克米每秒
0.05秒内停下:
F = Δp Δt
F = 180千克米每秒 0.05秒 = 3600牛顿
0.2秒内停下:
F = Δp Δt
F = 180 kg m/s 0.2 s = 900 N
慢点儿停下来需要的力小很多!
- 这就是为什么衬垫管用
- 为什么头盔可以保护性命
- 为什么汽车有碰撞缓冲区
问:力的公式不是 F = ma 吗?
答:其实 F =
Δp
Δt
是一样的,只是格式不同:
| 开始: | F = ma | |
| 加速度是速度 v 相对于时间 t的改变: | F = m Δv Δt | |
| 可以重排为: | F = Δmv Δt | |
| Δmv 是动量的改变: | F = Δp Δt |
由力产生的冲量
我们可以重排:
F = Δp Δt
为:
Δp = F Δt
所以我们可以计算在一段时间里施加力所产生的冲量(动量改变)。
例子:300牛顿的力打在球上。高速摄像机记录了接触时间是 0.02秒。冲量是多少?
Δp = F Δt
Δp = 300牛顿 × 0.02秒
Δp = 6牛顿秒
动量守恒
守恒:总量不变(在封闭系统里)。
封闭系统:无任何东西进入或离开,也无外力施加在系统上。
注意:在原子尺度,质量和能量可以以这个公式互相转换:E=mc2,总量还是不变的。
动量是矢量
动量是矢量:它有大小和方向。
有时我们不提到方向,但有时方向是重要的!
一维
一个一维的问题只需要正或负动量的答案:
二维或以上
但问题也可以是二维(或以上)的:
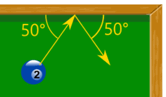
例子:台球反弹!
台球以 8 m/s 的速度及 50°的角度撞到球桌的边缘,然后以同样的速度和角度反弹回来。
台球的重量是 0.16 kg。动量的改变是多少?
我们先把速度分解成 x 与 y 部分。碰撞前:
- vx = 8 × cos(50°) ……向右
- vy = 8 × sin(50°) ……向上
反弹后:
- vx = 8 × cos(50°) ……向右
- vy = 8 × −sin(50°) ……向下
x速度没有改变,但 y速度改变了:
Δvy = (8+8) × sin(50°)
= 16 × sin(50°)
动量的改变是:
Δp = m Δv
Δp = 0.16 kg × 16 × sin(50°) m/s
Δp = 1.961…… kg m/s
动画
在这个动画里玩玩动量。
