递增与递减函数
递增函数
函数 是 "递增"函数,若然当 x值增大时,y值也增大:
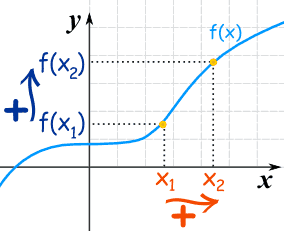
可以看到 y=f(x) 向右走时也同时向上走。
平坦?
但在开始时函数是平坦的,这可以吗?
- 如果是递增函数,这是允许的
- 但如果是严格递增函数(不允许有平坦部分)就不行了
用代数
如果我们不能为函数绘图呢?我们怎样知道是不是递增函数?在这个情况下,我们需要用代数来定义。
设 y=f(x):
| 若 x1 < x2,则 f(x1) ≤ f(x2) | 递增 | |
| 若 x1 < x2,则 f(x1) < f(x2) | 严格递增 |
一定要任何 x1 和 x2 都符合这个条件,不能只是某些 x值。
重点是 < 和 ≤ 符号 …… 记住它们的位置!
例子:
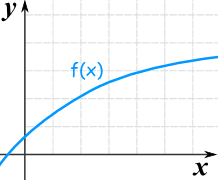 |
| 这也是个递增函数, 虽然增长率逐渐减小 |
区间
通常我们有兴趣的是一个区间:
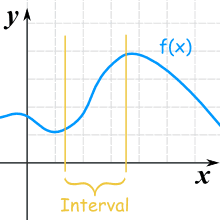
这个函数在图中的区间里是递增的
(在其它区间可能递增或递减)
递减函数
当 x值增大,y值减小:
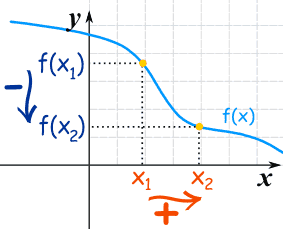
设 y=f(x):
| 若 x1 < x2,则 f(x1) ≥ f(x2) | 递减 | |
| 若 x1 < x2,则 f(x1) > f(x2) | 严格递减 |
注意 f(x1) 大于(或等于) f(x2)。
例子
我们现在来寻找一个函数在哪里递增和递减。
例子:f(x) = x3-4x,x 在区间 [−1,2] 里
我们画个图,包括区间 [−1,2]:
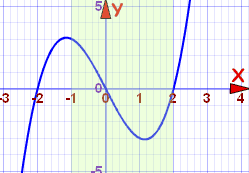
从 −1 开始(区间 [−1,2] 的起点):
- 在 x = −1,函数递减,
- 它一路递减,直到大约 1.2
- 然后开始递增,通过 x = 2
没有精确的分析,我们不知道曲线在哪里由递减变为递增,所以我们只能说:
在区间 [−1,2]里:
- 曲线在区间 [−1, 大约 1.2] 里递减
- 曲线在区间 [大约 1.2, 2] 里递增
常数函数
常数函数是条水平线:
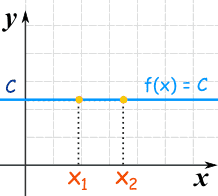
直线
直线是递增、递减或恒定的。
直线的方程是:
y = mx + b
坡度(斜率)m 显示函数是递增的、递减的或恒定的:
|
 |
一对一
严格递增(和严格递减)函数有个特别的属性,叫 "单射",也叫 "一对一",意思是在函数的输出里,同一个 "y" 值只能出现一次
| 一般函数 | "单射"(一对一) |
有什么用?我们可以可以倒转单射函数!
我们可以从 "y" 值还原为一个 "x"值(但如果同一个 y值有多于一个 "x值" 就不可以这样做了)。
去阅读单射、满射和双射了解更多。