e(欧拉数)

数字 e 是个有名的无理数,它是数学里最重要的数字之一。
首几个数位是:
2.7182818284590452353602874713527(无穷继续……)
通常称为欧拉数,以莱昂哈德·欧拉命名。
e 是自然对数的底(由约翰·纳皮尔发明)。
e 出现在很多数学领域里,所以了解它是很有用的。
计算
有很多计算 e 的值的方法,但没有方法可以算出绝对精确的值,因为 e 是个无理数(不是两个整数的比)。
但我们知道它精确到一万亿个小数位的值!
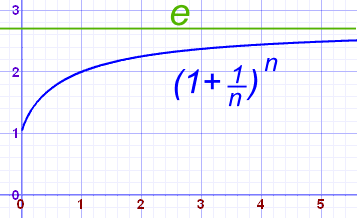
例如,当 n 越来越大时,(1 + 1/n)n 的值越来越趋近 e:
| n | (1 + 1/n)n |
| 1 | 2.00000 |
| 2 | 2.25000 |
| 5 | 2.48832 |
| 10 | 2.59374 |
| 100 | 2.70481 |
| 1,000 | 2.71692 |
| 10,000 | 2.71815 |
| 100,000 | 2.71827 |
另一个算法
e 也等于 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + 1/6! + 1/7! + ……
(注意:"!" 的意思是 阶乘)
首几项的和是:1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 = 2.718055556
你可以去综合计算器试试。
巧记
要记住 e 精确到十位小数的值,记住这个英语句子(数每个单词有几个字母):
- To
- express
- e
- remember
- to
- memorize
- a
- sentence
- to
- simplify
- this
你也可以记住在 "2.7" 后,"1828" 连续出现两次:
2.7 1828 1828,
然后就是等腰直角三角形的内角 45°、90°、45°:
2.7 1828 1828 45 90 45
(记得 e 的值是个很了不起的成就!)
有趣的属性
尝试 "分开然后相乘"
假设把一个数分成相等的部分,然后把所有部分相乘。
例子:把 20 分开为 4份,然后把它们相乘:
每 "份" 是 20/4 = 5
5×5×5×5 = 54 = 625
……问题是,每个部分要多大才可以得到最大的乘积?
例子(续):尝试 5 份:
每"份" 是 20/5 = 4
4×4×4×4×4 = 45 = 1024
好,答案大了!但是,怎样得到最大的答案?
答案:每部分的大小等于 "e"(或尽量接近 e)。
例子:10
| 10 分开为 3 份是 3.3…… | 3.3……×3.3……×3.3……(3.3……)3 = 37.037…… |
| 10 分开为 4 等份是 2.5 | 2.5×2.5×2.5×2.5 = 2.54 = 39.0625 |
| 10 分开为 5 等份是 2 | 2×2×2×2×2 = 25 = 32 |
最接近 "e" 的数值的乘积最大,这数值是 2.5。
自己来试试,比方用 100 …… 答案是多少?
高级:e 在复利计算里的应用
e 时常在意料不到的地方出现。
例如,计算借贷和投资的连续复利时,需要用到 e:
![]()
连续复利公式
为什么?
定期复利的公式是:
FV = PV (1+r/n)n
其中 FV = 终值
PV = 现值
r = 年利率(以小数表示)
n = 期数
期数越来越大时会怎么样?
留意下面两个公式的相似之处:
| (1+r/n)n | 和 | (1 + 1/n)n |
| 复利公式 | e(当 n 趋近无穷大) |
代入 x = n/r :
- r/n 变成 1/x,
- n 变成 xr
所以:
| (1+r/n)n | 变成 | (1+(1/x))xr |
这就是e 的公式(当 n 趋近无穷大时)加上一个指数 r。
因此,当 x 趋近无穷大时,(1+(1/x))xr 趋近 er
这就是为什么 e 出现在利息计算里!
超越数
e 也是个超越数 。