活动：抛硬币到方格上
几百年前人们喜欢 抛硬币到地上来赌博。。。。。。硬币会不会接触到地板上的线条呢？
乔治-路易·勒克莱尔，布丰伯爵 (Georges-Louis Leclerc, the Count of Buffon, 见 "布丰投针问题") 思考这问题，并算出了概率。
现在你来试试！
你需要：
   |
一枚小圆形硬币, 例如 美金 1 分，1 分 欧元 或 5 卢比。 |
 |
一张有格子的纸，方格每边 30 毫米长。 |
步骤
- 测量硬币的直径: ____ 毫米
- 美金 1 分是 19 毫米, 1 分 欧元是 16.25 毫米, 5 卢比是 23 毫米
- 测量方格的大小 （可能不是正好 30 毫米）： ____ 毫米
- 把纸张放在平面上，比方桌面或地板上。
- 从大概 5 厘米的高度，让硬币掉到纸上，记下它的落点：
A: 完全在方格内（不接触任何格线）
B: 横越一条或以上线条
从什么高度掉下硬币并不重要，但不要离纸张太近，这样是作弊！
若硬币滚到纸张外，不要计算这次.
100 次
我们现在要抛 100 次，不过在开始前。。。。。。
。。。。。。 A 和 B 的百分比是什么？
做实验前请先作一个猜测：
| 你猜 "A" 是 (%): | |
| 你猜 "B" 是 (%): |
好，我们开始。
抛硬币 100 次，用计数符号 记录下 A (不触线) 或 B (触线) :
| 硬币落点 | 计数符号 | 次数 | 百分比 |
|
A
|
|||
|
B
|
|||
| 总值： | 100 | 100% |
画一个柱状图来 显示说明你的实验结果。 你可以在 Data Graphs (Bar, Line and Pie) 生成柱状图。
- 柱状图里的柱是不是一样高？
- 你认为它们会一样高吗？
- 比对一下实验结果和你的猜测，你看到什么？
我们可以计算百分比的理论值是什么。。。。。。
这是一些硬币位置，在这些位置，硬币差点碰到 线条：
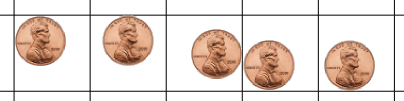
把硬币如上放在纸上，硬币差点碰到线条，再在硬币中心的位置做个记号 (位置差不多就可以了）。
 |
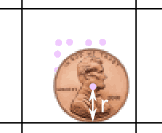硬币的中心和其中一条线的距离是一个半径。 （在这里看看关于圆形的 半 径和直径。） |
做很多硬币中心的记号，然后把它们连起来，画成一个框框。
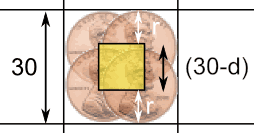
d = 硬币直径 (2 × r)
当硬币的中心在黄框子内，硬币便不会接触到 任 何线条。
黄框子比方格要短两个硬币的半径 （= 一个直径）。
面积是什么？
- 方格的面积是 30 × 30 = 900 平方毫米
- 黄框子的面积是 (30-d) × (30-d) = (30-d)2& 平方毫米
上面是用 30 mm 的方格来计算，我们可以用 S 来代表方格一边的长度：
- 方格的面积是 S × S = S2 平 方毫米
- 黄框子的面积是 (S-d)2 平方毫米
例子： 欧元1分硬币 （d=16.25 mm） ，29mm 格子 （S=29 mm）：
方格 = 292 = 841 平方毫米
黄框子 = (29−16.25)2 = 12.752 = 162 平方毫米 （到最近的平方毫米）
那么，硬币落在纸上而不碰到格线的可能性是差不多：
"A" = 162 / 841 = 19.3%
同样， "B" = 100% − 19.3% = 80.7%
现在用你做实验的方格和硬币大小来计算。
| 方格大小S （毫米）： | |
| 硬币直径 d （毫米）： | |
| 方格面积 = S2 （平方毫米）： | |
| 黄框子面积 = (S-d)2 （平方毫米）： | |
| "A" (%): | |
| "B" (%): |
这些理论值和你的实验结果比较起来怎么 样？
这不会是绝对准确的（因为这是随机的），但可能相差不大。
不同大小的硬币
试试用不同大小的硬币做这个实验。
- 先计算理论值。。。。。。这对 A 和 B 的可能性百分比有什么影响？
- 再做实验，看看结果有多准确。
你在这项活动中：
开开心心（希望是吧）做实验。
做了一些几何，并得到一些计算面积和概率的经验。
还体会到理论和现实的关系。