活动: 画正方形

这个活动只需要点网格、铅笔和脑筋。

我们来探索一下你在下边可以画多少个正方形：

注意： “1 乘 1” 是 边 的长度 （不是点的数目）。

现在我们来画一些正方形并数数有几个：

1 乘 1

很容易，是不？这是一个：

2 乘 2

那也容易。 总共有四个，对不对？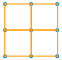
等一等，还有。 还有一个大的：

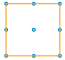总共五个――四个 1 乘 1 的正方形和一个 2 乘 2 的正方形

轮到你了！

3 乘 3

你来画。 这是点网格：

 

 

现在你可以做个列表：

	多少个 1 乘 1 正方形	多少个 2 乘 2 正方形	多少个 3 乘 3 正方形	多少个 4 乘 4 正方形	多少个 5 乘 5 正方形	总数
1 乘 1 点网格：	1					1
2 乘 2 点网格：	4	1				5
3 乘 3 点网格：
4 乘 4 点网格：
5 乘 5 点网格：

 

你在表上的数字留意到什么？

它们全是 平方数：

• 1² = 1,
• 2² = 4,
• 3² = 9,
• 等等。。。。。。

总数就是平方数的和。

有公式可以帮到你。。。。。。！

其实有一个 公式 来计算头 n 个平方数的和：

S_n = n(n+1)(2n+1) / 6

 

我们好像解决问题了。 好哇！

可是，等等。。。。。还有呢！

我不是说过你要动脑筋吗？ 我们再看看 2 乘 2 的例子：

2 乘 2

还有一个正方形呢，这个：

所以总共有六个正方形。

四个 1 乘 1 正方形、一个2 乘 2 正方形和一个 x 乘 x 正方形。

所以有 四个 1 乘 1 正方形， 一个 2 乘 2 正方形 和 一个 √2 乘 √2 正方形.

轮到你了！

3 乘 3

• 还有更多正方形吗？

有！ 你能不能找到？

4 乘 4 和 5 乘 5

也来试试 4 乘 4 和 5 乘 5 点网格！

你做下去，会发现有这样的正方形：

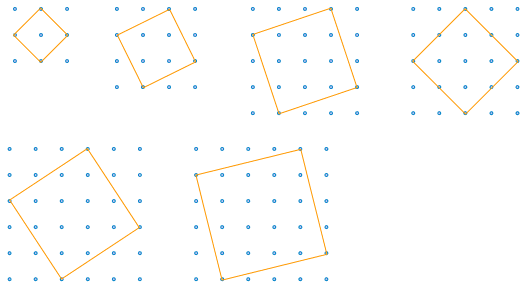
这些正方形的边长是什么？

你可也用 勾股定理 来计算

在每个例子里，每种正方形你找到几个？

以下的列表可以帮到你：

多少个 1 乘 1

多少个 2 乘 2

多少个 3 乘 3

多少个 4 乘 4

多少个 5 乘 5

多少个 √2 乘 √2

多少个 √5 乘 √5

多少个 √8 乘 √8

多少个 √10 乘 √10

多少个 √13 乘 √13

多少个 √17 乘 √17

总数

1 乘 1 点网格:

1

1

2 乘 2 点网格:

4

1

1

6

3 乘3 点网格:

4 乘 4 点网格:

5 乘 5 点网格:

 

高等问题

你可不可以找到一个公式去计算有多少个边长为平方根的正方形？

你可不可以找到一个公式去计算每个例子有多少个正方形？

有没有我们仍然忽视了的正方形？

结论

当初好像是很简单的习题原来是相当复杂的。 你真的 要 动动脑筋去仔细想想这个，不过这个很有挑战性和价值。